こんにちは。今回は平面ベクトルの必須アイテム, 分点の公式を扱っていきます。線分AB上に点Pがある場合(Pが内分点の場合)と点Pが線分AB外側で直線AB上にある場合(点Pが外分点の場合)を示していきます。
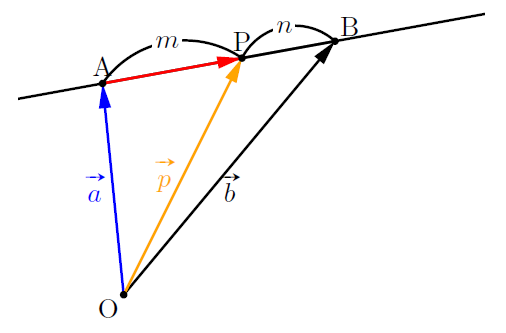
Pがm : nに内分する場合
まずは点Pが線分ABを![]() に内分する場合
に内分する場合
![]()
![]()
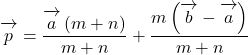
![]()
ちなみに, ![]() を書き換えると,
を書き換えると, ![]()
となり, 下線部の和は1(点Pが直線AB上にあるので)になっています。
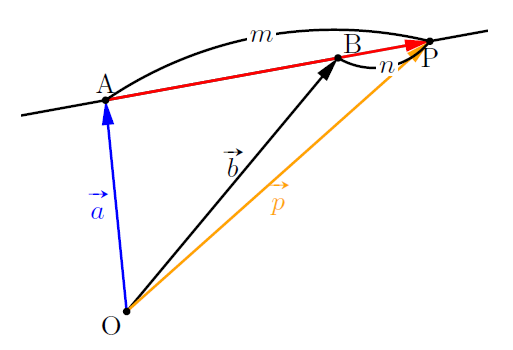
Pがm : n(m>n)に外分する場合
点Pが![]() に外分するとき,
に外分するとき,
![]()
![]()
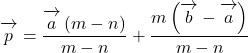
![]()
ちなみに, ![]() を書き換えると,
を書き換えると,![]()
となり, 下線部の和は1(点Pが直線AB上にあるので)になっています。
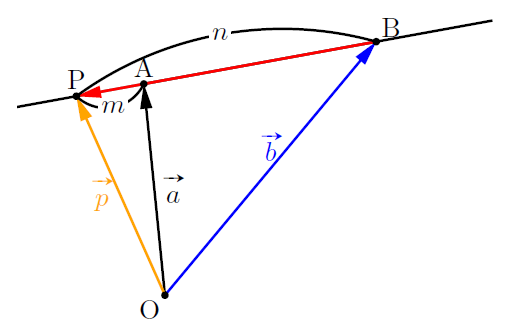
Pがm : n(m<n)に外分する場合
点Pが![]() に外分するとき,
に外分するとき,
![]()
![]()
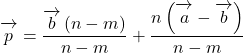
![]()
ちなみに, ![]() を書き換えると,
を書き換えると,![]()
となり, 下線部の和は1(点Pが直線AB上にあるので)になっています。
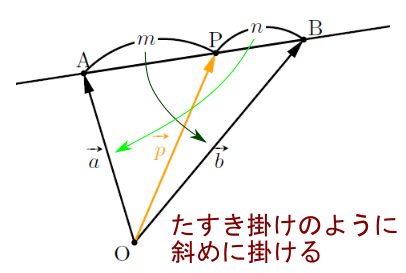
分点公式の覚え方
分点の公式は以下のように覚えるといいかもしれません。
外分点は![]() に内分すると考えて, 内分点と同じように扱うといいでしょう。
に内分すると考えて, 内分点と同じように扱うといいでしょう。
 数樂管理人のブログ
数樂管理人のブログ