こんにちは。今回は登場回数は低いもののいざというとき困るので, 覚えておきたい![]() の和の公式です。
の和の公式です。
n³の和の公式

私の覚え方:1~![]() までの和の2乗
までの和の2乗
![]() として辺々の和を1~
として辺々の和を1~![]() までとります。
までとります。
すなわち,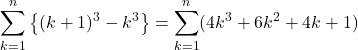
これを![]() から見ていくと
から見ていくと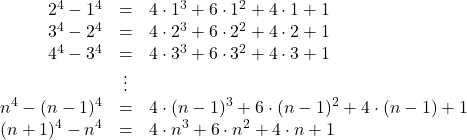
これらをすべて加えると, 4乗の項が打ち消し合っていくことが分かります。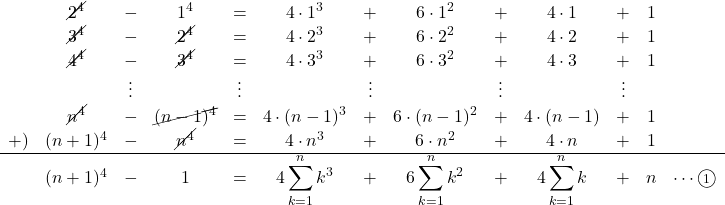
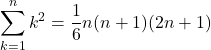 ,
, 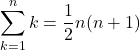 として,
として, ![]() を計算していくと,
を計算していくと,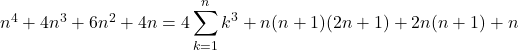
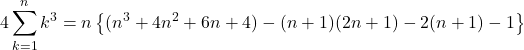
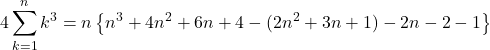
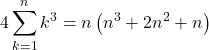
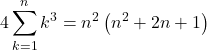
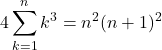
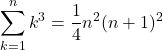
よって,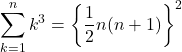
この導出方法を用いれば![]() の和の公式も導出できますね。
の和の公式も導出できますね。
それでは。
こんにちは。今回は登場回数は低いもののいざというとき困るので, 覚えておきたい![]() の和の公式です。
の和の公式です。

私の覚え方:1~![]() までの和の2乗
までの和の2乗
![]() として辺々の和を1~
として辺々の和を1~![]() までとります。
までとります。
すなわち,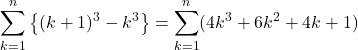
これを![]() から見ていくと
から見ていくと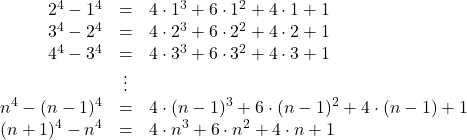
これらをすべて加えると, 4乗の項が打ち消し合っていくことが分かります。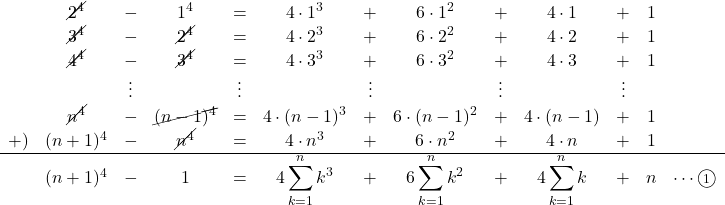
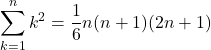 ,
, 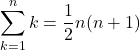 として,
として, ![]() を計算していくと,
を計算していくと,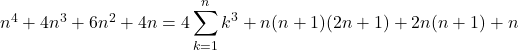
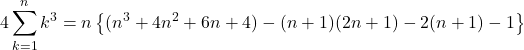
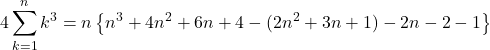
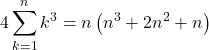
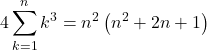
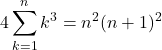
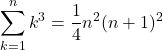
よって,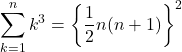
この導出方法を用いれば![]() の和の公式も導出できますね。
の和の公式も導出できますね。
それでは。