こんにちは。今回は累乗根について書いておきます。
![]() を自然数とすると,
を自然数とすると, ![]() 乗して,
乗して, ![]() になる数を
になる数を![]() の
の![]() 乗根という。ちなみに2乗して
乗根という。ちなみに2乗して![]() になる数は,
になる数は, ![]() の平方根といいます。
の平方根といいます。
例えば8の3乗根(立方根ともいう)の数は?と聞かれたら, この意味は3乗して8になる数字はいくつですか?と聞いていることと同意です。したがって, この場合, 8の3乗根は, ただ1つだけあって, 2になります。![]() ですから。
ですから。
同じように16の4乗根はというと, 4乗して16になる数字ですから, この場合, 正負の2つあって, ![]() になります。
になります。![]() ですから。
ですから。
それでは5の3乗根は?と聞かれたらこのような数字はないので, 平方根同様, 根号を使って表します。奇数乗根の値はただ1つしかないので, この場合, 5の3乗根は![]() と表します。
と表します。
同様に, 5の4乗根は?と聞かれたらこのような数字はないので, 先と同様, 根号を使って表しますが, 偶数乗根は正負の2つあるので, この場合, 5の4乗根は![]() となります。ただし, 負の数の偶数乗根は実数では存在しません。
となります。ただし, 負の数の偶数乗根は実数では存在しません。![]() が奇数のときと偶数のときで,
が奇数のときと偶数のときで, ![]() 乗根の値が1つだったり2つだったりする理由を見ていきましょう。
乗根の値が1つだったり2つだったりする理由を見ていきましょう。
![]() 乗根(
乗根(![]() が奇数のとき)
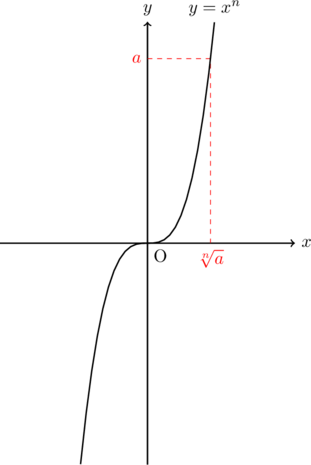
が奇数のとき)![]() は奇数)のグラフの概形は以下のようになり, 1つの
は奇数)のグラフの概形は以下のようになり, 1つの![]() 値に対して,
値に対して, ![]() の値はただ1つ決まる。したがって,
の値はただ1つ決まる。したがって, ![]() 乗根の値もただ1つ決まる。また, グラフから負の値の
乗根の値もただ1つ決まる。また, グラフから負の値の![]() 乗根も存在することがわかる。
乗根も存在することがわかる。
![]() 乗根(
乗根(![]() が偶数のとき)
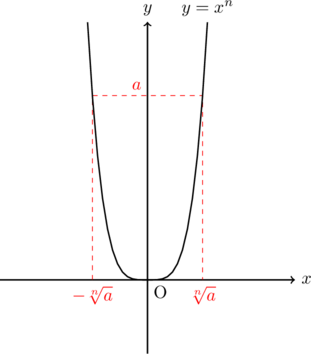
が偶数のとき)![]() は偶数)のグラフの概形は以下のようになり, 1つの
は偶数)のグラフの概形は以下のようになり, 1つの![]() 値に対して,
値に対して, ![]() の値は2つ決まる。したがって,
の値は2つ決まる。したがって, ![]() 乗根の値は2つあるが, グラフから負の値は存在しないので, 負の数の
乗根の値は2つあるが, グラフから負の値は存在しないので, 負の数の![]() 乗根の値も実数の範囲では存在しない。
乗根の値も実数の範囲では存在しない。
 数樂管理人のブログ
数樂管理人のブログ 


「グラフから負の値は存在しない」の部分がいまひとつ分かりません。
y=ax^(偶数)のyの値はグラフから0以上の値しかとらない。これはyが負の値を取ることはないので, 負の値の偶数乗根は実数では存在しないことを意味するということです。
間違ってたらすみません。