こんにちは。今回は![]() が
が![]() になった場合の三角関数の関係について書いておきます。
になった場合の三角関数の関係について書いておきます。
θがθ+π/2になると
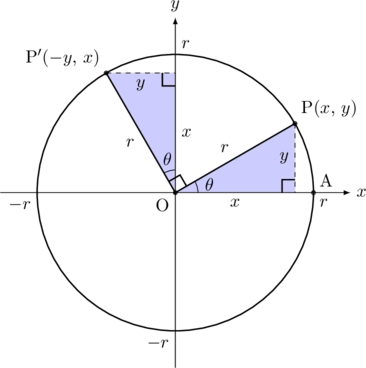
この手の導き方は円を用いた解法ですので, ぜひ身に付けておいてください。今, 動径OPと![]() 軸がなす角を
軸がなす角を![]() とし, 点Pの座標を
とし, 点Pの座標を![]() とする。この
とする。この![]() に
に![]() を加えた角を
を加えた角を![]() とし,
とし, ![]() とする。このとき,
とする。このとき, ![]() 軸と
軸と![]() 軸は直角に交わっているので,
軸は直角に交わっているので, ![]() 軸と動径OP
軸と動径OP![]() のなす角は
のなす角は![]() になっています。このことから, 色の付いた三角形は合同なので, P
になっています。このことから, 色の付いた三角形は合同なので, P![]() の座標は
の座標は![]() となります。
となります。
この結果を表にすると以下のようになり,
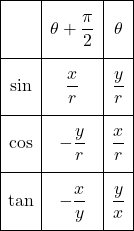
![]() は
は![]() と,
と, ![]() は
は![]() と,
と,![]() は
は![]() とそれぞれ対応させると, 次の関係が式ができます。
とそれぞれ対応させると, 次の関係が式ができます。![]()
![]()
![]()
このように公式を導くことができました。
θ+π/2の三角関数
 数樂管理人のブログ
数樂管理人のブログ 

