こんにちは。今回は三角関数を含む関数の最大値と最小値について書いておきます。例題を解きながら見ていきます。
【例①】関数![]()
![]() の最大値と最小値を求め, そのときの
の最大値と最小値を求め, そのときの![]() の値を求めよ。
の値を求めよ。
【解法】一見複雑そうですが, ![]() だけの最大値, 最小値を, 与えられた
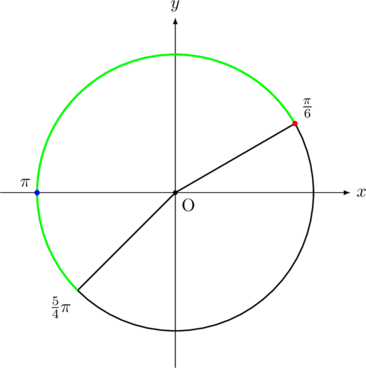
だけの最大値, 最小値を, 与えられた![]() の範囲(下図緑色の範囲)で考えればいいだけです。なぜなら,
の範囲(下図緑色の範囲)で考えればいいだけです。なぜなら, ![]() の値の大小が, 関数の値の大小に直結するから。そこで, 円を描いて考えると,
の値の大小が, 関数の値の大小に直結するから。そこで, 円を描いて考えると, ![]() だから,
だから, ![]() の値が最大のところが,
の値が最大のところが, ![]() の値も最大で,
の値も最大で, ![]() の値が最小のところが,
の値が最小のところが, ![]() の値も最小になる。したがって, 下図赤色の印が
の値も最小になる。したがって, 下図赤色の印が![]() 座標が最大になるので,
座標が最大になるので, ![]() の値も最大で, その値は,
の値も最大で, その値は, ![]() 。下図青色の印が
。下図青色の印が![]() 座標が最小になるので,
座標が最小になるので, ![]() の値も最小で, その値は,
の値も最小で, その値は, ![]() 。
。
以上より, ![]() の取りうる範囲は,
の取りうる範囲は, ![]()
関数の右辺は, ![]() なので, これを2倍して,
なので, これを2倍して, ![]()
次に各辺に![]() を加えて,
を加えて, ![]()
したがって,
関数の最大値は, ![]() のとき,
のとき, ![]() ,
,
最小値は, ![]() のとき,
のとき, ![]() となる。
となる。
【例②】関数
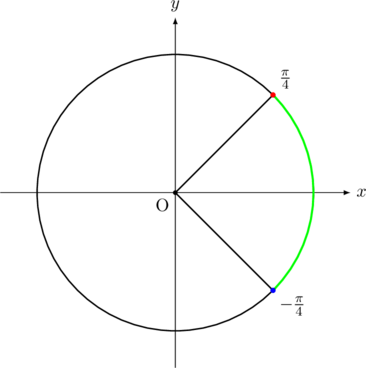
【解法】これは, 関数の
そこで範囲を再定義すると,
となり,
となり,
そのときの,
最大値を与える
最小値を与える
したがって,
関数の最大値は,
最小値は,
 数樂管理人のブログ
数樂管理人のブログ 

