TikZ：高校数学：三角関数を含む関数の最大値・最小値②

こんにちは。今回は三角関数を含む関数の最大値, 最小値について書いておきます。例題を解きながら見ていきます。

sinかcosのどちらかで置き換える

【例題】 $0\leqq\theta<2\pi$ のとき, 関数 $y=2\cos^2\theta-2\sin\theta$ の最大値と最小値を求め, そのときの $\theta$ の値も求めよ。
【解法】基本的に2乗の項を $\sin^2\theta+\cos^2\theta=1$ を使って, $\sin, \cos$ のどちらかの三角関数で置き換えて関数を書き直すのが定石です。そして, $\sin=t$ , または, $\cos=t$ とおいて, $\theta$ の範囲から $t$ の範囲を再定義し, 最大, 最小値を求めるというのが流れになります。
それでは, 流れに沿って解いていきましょう。
先ず, 2乗の項 $2\cos^2\theta$ 以外に $\sin\theta$ があるので, $\cos^2\theta=1-\sin^2\theta$ を使って, $\sin\theta$ だけで関数を書き直す。
$\begin{array}{lll}y&=&2\left(1-\sin^2\theta\right)-2\sin\theta\\&=&-2\sin^2\theta-2\sin\theta+2\end{array}$
$\sin\theta=t$ とおくと,
$y=-2t^2-2t+2$ となり,
$0\leqq\theta<2\pi$ より, $-1\leqq t\leqq1$ となる。
平方完成すると,
$y=-2\left(t+\dfrac12\right)^2+\dfrac52$
$-1\leqq t\leqq1$ の範囲でグラフをかいて調べると,

$t$ の範囲において, 最大値は $t=-\dfrac12$ のときで, $\dfrac52$ , 最小値は $t=1$ のときで, $-2$ になります。
$t=\sin\theta$ として, それぞれを与える $\theta$ を求めると,
$\sin\theta=-\dfrac12$ より, $\theta=\dfrac76\pi, \dfrac{11}{6}\pi$
$\sin\theta=1$ より, $\theta=\dfrac{\pi}{2}$
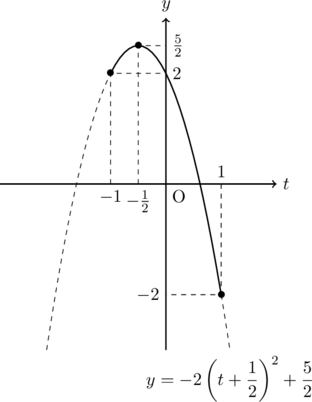
以上より,
最大値は $\theta=\dfrac76\pi, \dfrac{11}{6}\pi$ のとき, $\dfrac52$
最小値は $\theta=\dfrac{\pi}{2}$ のとき, $-2$

三角関数を含む関数の最大値・最小値

$\textcircled{\scriptsize 1}$ 　 $\sin^2\theta+\cos^2\theta=1$ などを用いて, $\sin\theta$ または $\cos\theta$ だけの関数に書き換える。
$\textcircled{\scriptsize 2}$ 　このとき, $\theta$ の範囲から $t$ の定義域を再度定義し直すのを忘れない。
$\textcircled{\scriptsize 3}$ 　 $t$ の定義域から最大値・最小値を求める。
$\textcircled{\scriptsize 4}$ 　必要なら, $t=\sin\theta$ または $t=\cos\theta$ から最大値・最小値を与える $\theta$ の値を求める。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル