こんにちは。今回はベクトルと内分点ということで, 比較的重要な例題をやっておきます。それでは見ていきましょう。
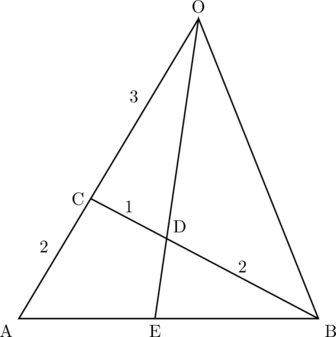
【例】△OABにおいて, 辺OAを![]() に内分する点をC, 線分BCを
に内分する点をC, 線分BCを![]() に内分する点をDとし, 直線ODと辺ABの交点をEとする。このとき,
に内分する点をDとし, 直線ODと辺ABの交点をEとする。このとき, ![]() を
を![]() ,
, ![]() で表し, OD : DEを求めよ。
で表し, OD : DEを求めよ。
【解法】OD : DEだけならメネラウスの定理を使えば出せますが, それは今回は無しということでいきます。
CD : DB=1 : 2なので,
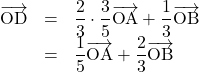
よって,
ここで,
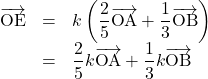
Eは辺AB上にあるので,
これを解いて,
よって,
したがって, OD : DE
【別解】
を次のように変形することもできる。
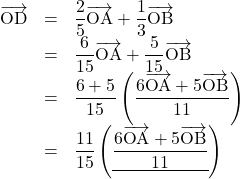
下線部は
よって, OD : DE
 数樂管理人のブログ
数樂管理人のブログ 

