高校数学：ベクトルの内積の角ってなんで180°までなの？

こんにちは。今回はベクトルの内積で, 2つのベクトルがなす角を表すときに, なのでって断りが入るのですが, 越えちゃダメなの？って話です。

結局同じことだから

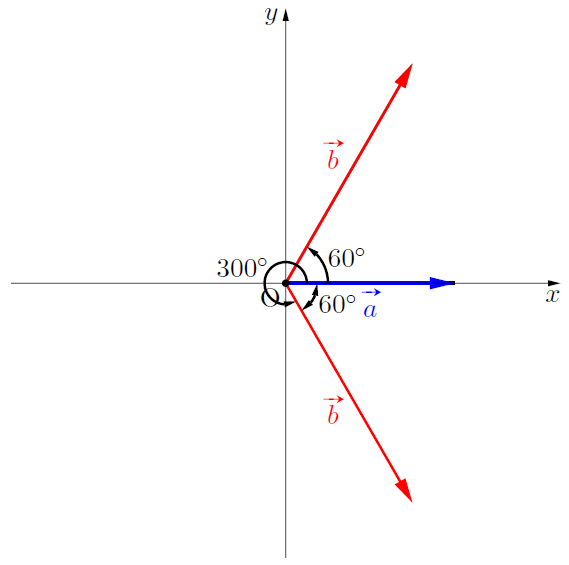
ベクトルのなす角をからに広げてみます。そこで, ベクトルのなす角を求めようと, の値を求めると, であったとすると, 図のように, または, となるわけですが, のなす角は, 小さい方の角で考えると, と言えます。したがって, わざわざの範囲を広げて, の角を求める必要性がないということでしょうね。
このようにの範囲を広げたところで, 求まる2つのの和が360になるので, あまり意味をなさない。紛らわしいだけということですね。それでは。