高校数学：軌跡の基本的な解法③

こんにちは。相城です。今回は軌跡の基本的な解法の第3弾です。例題を見ながらいきましょう。

軌跡の基本的な解法③

【例】 $t$ がすべての実数値をとって変化するとき, 次の式で表される点( $x, y$ )はどのような図形上を動くか求めよ。
$x=2t, y=4t^2-3t+1$
【解法】 $x=2t$ を $t$ について解き, $y$ に代入する。
与式から, $t=\dfrac{x}{2}$ なので, これを $y$ に代入すると,
$y=4\cdot\left(\dfrac{x}{2}\right)^2-3\cdot\dfrac{x}{2}+1$
$y=x^2-\dfrac32x+1$
よって, 点( $x, y$ )は放物線 $y=x^2-\dfrac32x+1$ 上を動く。

解法のコツ

片方の式を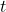 $t$ について解き, もう片方に代入して 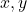$x, y$ の関係式をつくる。

【例】 $t$ がすべての実数値をとって変化するとき, 放物線 $y=x^2-2(t+2)x+3t^2+t$ の頂点Pの軌跡を求めよ。
【解法】まずは平方完成する。
$\begin{array}{lll}y&=&\left\{x-(t+2)\right\}^2-(t+2)^2+3t^2+t\\&=&\left\{x-(t+2)\right\}^2+2t^2-3t-4\end{array}$
よって, 頂点の座標Pを( $x, y$ )とすると,
$x=t+2\cdots\textcircled{\scriptsize 1}$
$y=2t^2-3t-4\cdots\textcircled{\scriptsize 2}$
となり,
$\textcircled{\scriptsize 1}$ から,
$t=x-2$ となり, これを $\textcircled{\scriptsize 2}$ に代入すると,
$\begin{array}{lll}y&=&2(x-2)^2-3(x-2)-4\\&=&2x^2-11x+10\cdots\textcircled{\scriptsize 3}\end{array}$
よって, 点Pはこの放物線 $\textcircled{\scriptsize 3}$ 上にある。
したがって, 求める点Pの軌跡は放物線 $y=2x^2-11x+10$