高校数学：2つの円の位置関係

こんにちは。今回は2つの円の位置関係について書いておきます。公式を覚えやすいようにまとめてみたのでよかったら使ってみてください。

公式を1行にまとめました

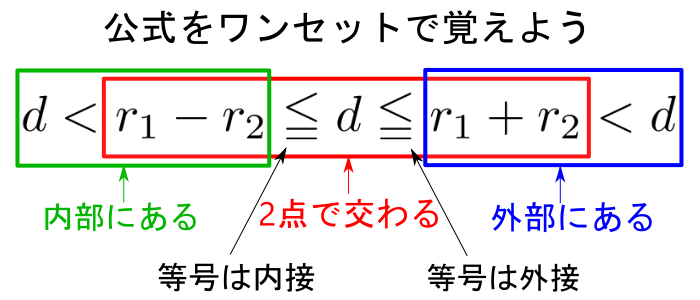
覚える公式をまとめて1つの公式にしました。
円の半径を $r_1, r_2\ (r_1>r_2)$ とし, 中心間の距離を $d$ とすると,
$d<r_1-r_2\leqq d\leqq r_1+r_2<d$
この不等式の見方は次のようです。
内部にある $<r_1-r_2<$ 2点で交わる $<r_1+r_2<$ 外部にある
等号は $r_1-r_2=d$ は内接, $r_1+r_2=d$ は外接を表す。

例題をやってみよう。
【例】2つの円 $(x-2)^2+y^2=9\cdots\textcircled{\scriptsize 1}$ , $(x-1)^2+(y+1)=4\cdots\textcircled{\scriptsize 2}$ の位置関係を調べよ。
【解法】2つの円の半径は3, 2で, 中心はそれぞれ, (2, 0), ( $1, -1$ )である。
上の不等式を用いると,
$d<3-2\leqq d\leqq 3+2<d\Longrightarrow d<1\leqq d\leqq5<d$
中心間の距離 $d$ を求めると,
$d=\sqrt{(2-1)^2+(0+1)^2}=\sqrt2$
この長さは上の不等式の範囲でいうと, 1と5の間の数字なので, 円 $\textcircled{\scriptsize 1}$ と円 $\textcircled{\scriptsize 2}$ は2点で交わることが分かります。

【例】2つの円 $x^2+y^2=16\cdots\textcircled{\scriptsize 1}$ , $(x-1)^2+(y+1)=4\cdots\textcircled{\scriptsize 2}$ の位置関係を調べよ。
【解法】2つの円の半径は4, 2で, 中心はそれぞれ, (0, 0), ( $1, -1$ )である。
上の不等式を用いると,
$d<4-2\leqq d\leqq 4+2<d\Longrightarrow d<2\leqq d\leqq6<d$
中心間の距離 $d$ を求めると,
$d=\sqrt{(0-1)^2+(0+1)^2}=\sqrt2$
この長さは上の不等式の範囲でいうと, 2より小さい数字なので, 円 $\textcircled{\scriptsize 2}$ は円 $\textcircled{\scriptsize 1}$ の内部にあることが分かります。

【例】2つの円 $(x-1)^2+y^2=1\cdots\textcircled{\scriptsize 1}$ , $(x-4)^2+(y-4)=16\cdots\textcircled{\scriptsize 2}$ の位置関係を調べよ。
【解法】2つの円の半径は1, 4で, 中心はそれぞれ, (1, 0), (4, 4)である。
上の不等式を用いると,
$d<4-1\leqq d\leqq 4+1<d\Longrightarrow d<3\leqq d\leqq5<d$
中心間の距離 $d$ を求めると,
$d=\sqrt{(1-4)^2+(0-4)^2}=5$
この長さは上の不等式の範囲でいうと, 5と等しい数字なので, 円 $\textcircled{\scriptsize 1}$ と円 $\textcircled{\scriptsize 2}$ は外接することが分かります。

このような感じで問題に取り組んでみてください。
それでは。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル