こんにちは。今回はある領域において, 式のとる値の最大値, 最小値について調べてみたいと思います。典型パターンを記しておきます。
【例題】![]() ,
, ![]() が4つの不等式
が4つの不等式![]() ,
, ![]() ,
, ![]() ,
, ![]() を同時に満たすとき,
を同時に満たすとき, ![]() の最大値と最小値を求めよ。
の最大値と最小値を求めよ。
【解法】まずは4つの不等式の表す領域を図示する。![]() より,
より, ![]()
![]() より,
より, ![]()
これらと, ![]() ,
, ![]() より, 4つの不等式が表す領域は下図の色を付けた部分(境界線は含む)である。
より, 4つの不等式が表す領域は下図の色を付けた部分(境界線は含む)である。
2つのグラフ![]() と
と![]() のグラフの交点は
のグラフの交点は![]() である。
である。
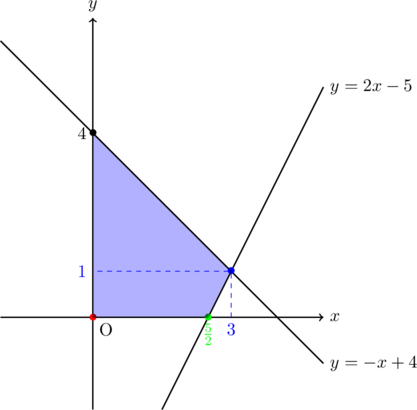
ここで
それを図示すると,
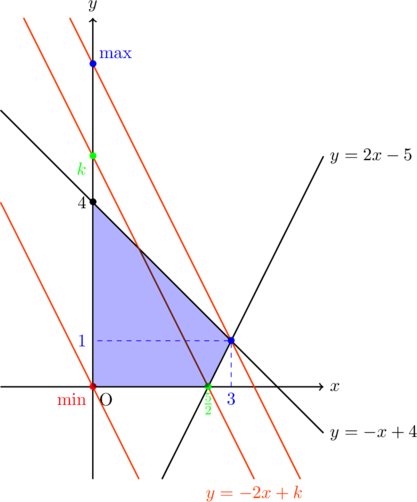
このように切片
以上より,
このような感じで解いていきます。
解法の流れ
![]()
![]() のとる領域を図示する。
のとる領域を図示する。![]() 求める値を
求める値を![]() とおき,
とおき, ![]() について解き,
について解き, ![]() の値を関数
の値を関数![]() の一部として扱う。
の一部として扱う。
今回は切片になる。![]() 領域のどこを通るのが最大, 最小になるか調べて答える。
領域のどこを通るのが最大, 最小になるか調べて答える。
 数樂管理人のブログ
数樂管理人のブログ 


