こんにちは。今回は対数を含む不等式で底が1より小さい正の数のとき, なぜ不等号の向きが変わるのか。それについて触れておきたいと思います。
まず底が1より大きい場合の例をやってみます。
【例】![]() を解け。
を解け。
【解法】問題が聞いていることは, ![]() のグラフで1より大きいい範囲を求めなさいということです。以下グラフと合わせながら見ていきます。
のグラフで1より大きいい範囲を求めなさいということです。以下グラフと合わせながら見ていきます。
真数条件より![]()
与式は, ![]() と考えることができます。
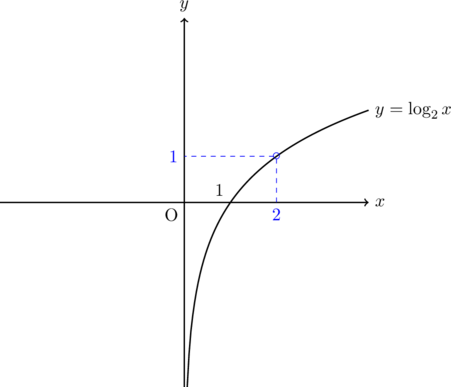
と考えることができます。 ![]() のグラフは以下のようで,
のグラフは以下のようで, ![]() は青印のところ。不等号はそれより大きい部分を求めているので,
は青印のところ。不等号はそれより大きい部分を求めているので, ![]() より大きい範囲になります。したがって,
より大きい範囲になります。したがって, ![]() 。真数条件と合わせて
。真数条件と合わせて![]() (答)
(答)
不等号の向きが変わらないのは, グラフが単調増加(ずっと右上がりのグラフ)だからです。
ですから底が1より大きいとき, 真数条件の考慮をして, 単純に![]() とできます。
とできます。
次に底が
【例】
【解法】問題が聞いていることは,
真数条件より
与式は,
不等号の向きが変わるのは, グラフが単調減少(ずっと右下がりのグラフ)だからです。
ですから底が1より小さい正の数のとき, 真数条件の考慮を入れたとしても, 単純に
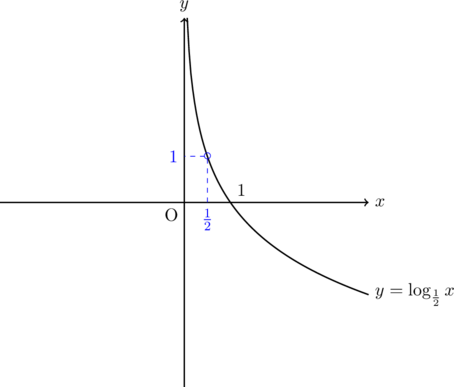
このように底が1より小さいとグラフが右下がりになるので, 不等号の向きが逆になります。その点注意が必要ですね。では。
 数樂管理人のブログ
数樂管理人のブログ 

