高校数学：組分けの問題

こんにちは。相城です。今回は場合の数のところで出てくる組分けの問題に関してです。例題を解きながら見ていきましょう。

組分け問題

【例題】6人を次の組に分ける方法は何通りありますか。
(1)　2人ずつA, B, Cの3つのグループに分ける方法
(2)　2人ずつ3つのグループに分ける方法
【解法】
(1)はグループに区別があります。Aのグループには6人から2人選んで入れて, Bグループには残りの4人から2人選んで入れて, Cグループは残り2人を(自動的に)入れる。これらは同時に起こるので, 計算式は
${}_6\mathrm{C}_2\times{}_4\mathrm{C}_2=90$
90通り
(2)は(1)のA, B, Cのグループを取り払って2人ずつ分けるだけの場合。今6人をa, b, c, d, e, fとして, 2人ずつ, (a, b), (c, d), (e, f)の3組に分けます。 A, B, Cの区別がある場合, この3組の並びは以下のようになります。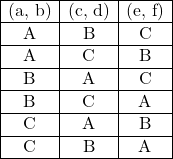
$\begin{array}{|c|c|c|} \hline(\text{a, b})&(\text{c, d})&(\text{e, f})\\ \hline \text{A}&\text{B}&\text{C}\\ \hline \text{A}&\text{C}&\text{B}\\ \hline \text{B}&\text{A}&\text{C}\\ \hline \text{B}&\text{C}&\text{A}\\ \hline \text{C}&\text{A}&\text{B}\\ \hline \text{C}&\text{B}&\text{A}\\ \hline\end{array}$
このように(a, b), (c, d), (e, f)と分けてA, B, Cの区別をつけると6通りの並びができます。しかし今回はこの6通りの区別がないので, これら6つすべて同じ組として考えます。したがって, (1)で求めた値を6( $3!$ )で割らなくてはなりません。よって, 求める答えは
$\begin{array}{rcl}\dfrac{{}_6\mathrm{C}_2\times{}_4\mathrm{C}_2}{3!}&=&\dfrac{90}{6}\\&=&15\end{array}$
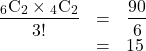
15通り
【例題】5人を1人, 2人, 2人の組に分ける方法は何通りありますか。
【解法】上の問題の(2)の問題と同じですが, 組の人数が多少異なります。
2人の2組に区別がないので, 3つの異なる並びを考えてそれを $2!$ (区別のない2組)で割ればいいので, 求める場合の数は,
$\begin{array}{rcl}\dfrac{{}_5\mathrm{C}_2\times{}_3\mathrm{C}_2}{2!}&=&\dfrac{30}{2}\\&=&15\end{array}$
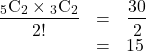
15通り

このような感じで求めていきます。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル