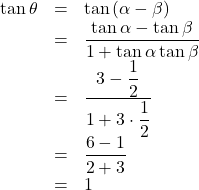こんにちは。今回は![]() の加法定理を用いた2直線のなす角について書いておきます。例題を解きながら見ていきます。
の加法定理を用いた2直線のなす角について書いておきます。例題を解きながら見ていきます。
例題を見ていこう
【例題】2直線![]() ,
, ![]() のなす角
のなす角![]() を求めよ。ただし,
を求めよ。ただし, ![]() は鋭角とする。
は鋭角とする。
【解法】先ずは与式を![]() について解き, グラフを描いて様子を見る。
について解き, グラフを描いて様子を見る。
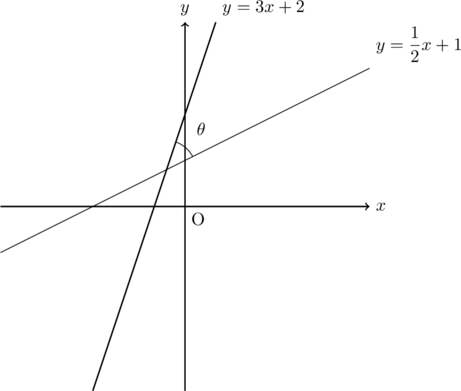
グラフ中の
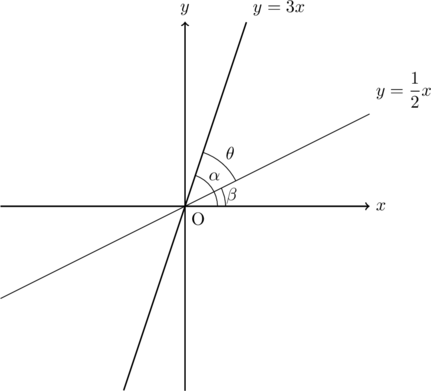
このとき,
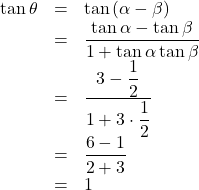
よって
このような感じで求めていきます。
こんにちは。今回は![]() の加法定理を用いた2直線のなす角について書いておきます。例題を解きながら見ていきます。
の加法定理を用いた2直線のなす角について書いておきます。例題を解きながら見ていきます。
例題を見ていこう
【例題】2直線![]() ,
, ![]() のなす角
のなす角![]() を求めよ。ただし,
を求めよ。ただし, ![]() は鋭角とする。
は鋭角とする。
【解法】先ずは与式を![]() について解き, グラフを描いて様子を見る。
について解き, グラフを描いて様子を見る。