数樂管理人のブログ 
こんにちは。今回は正負の数の応用・平均の求め方について書いておきます。
あるクラスの5人の身長を測定した。下の表は168cmを基準にそれより高い生徒は正の数で, それより低い生徒は負の数で表したものである。このとき, 5人の平均身長を求めなさい。
中1年生でよく出てくる問題です。ここで, この問題で問われている平均の求め方は, 次の方法で求めることができます。
(平均)
(基準)
(表の平均)
すなわち、この問題の答えは
(cm)
それはなぜか考えてみましょう。基本は小学生の平均の考え方です。
小学校の時, 平均は以下のように教わったかもしれません。
(平均)(合計)
(個数)
この小学校の平均では基準がすべて0なんです。例えば国語70点、数学60点、英語80点の3科目の平均点は
と聞かれると, 
(点)です。
基準を変えることもできます。基準を50にすると, 次のような 表にまとめることができる。
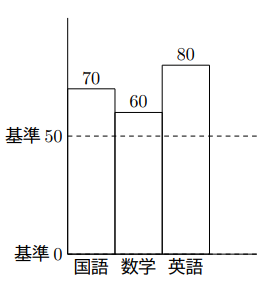
ここで、(平均)(基準)(表の平均)を使ってみると、
(平均)
(点)
さっきと同じになりました。
同じ原理で、基準を動かすことができます。例えば基準が100でもです。負の数を習ったからです。
基準を100にすると, 次の表のようにまとめることができます。
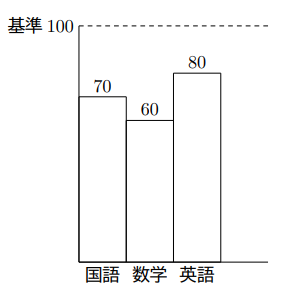
ここで, (平均)(基準)(表の平均)を使ってみると,
(平均)
(点)
同じです。こうやって負の数を習ったことで, 基準を自由に動かすことができ, 小学校のように
数字そのままを加えていくのではなく, 一定の基準を設け, 扱う数字を抑え計算の効率を上げることができます。
今回の解き方では, 前日を基準とする場合の問題には適合しないので, 気を付けてください。ただ前日を基準とする問題もある特定の日などを基準とし, 表を作り直すことで同じように解くことができます。
それでは。
