こんにちは。今回は数列の基本公式![]() と
と![]() の導出を書いておきます。最後に使い道を示しておきます。
の導出を書いておきます。最後に使い道を示しておきます。
![]()
![]()
![]() より
より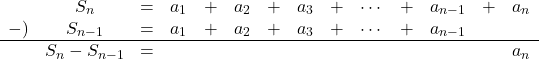
よって, ![]()
同様にして, ![]()
![]()
![]() より
より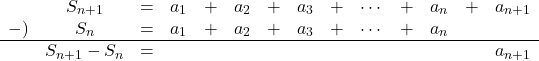
よって,![]()
以上になります。
漸化式で![]() が登場するときや, 漸化式に
が登場するときや, 漸化式に![]() が登場するときに使うと効果的です。使い方としては, 基本1つずらして引くことだけですので, 効果てきめんです。
が登場するときに使うと効果的です。使い方としては, 基本1つずらして引くことだけですので, 効果てきめんです。
こんにちは。今回は数列の基本公式![]() と
と![]() の導出を書いておきます。最後に使い道を示しておきます。
の導出を書いておきます。最後に使い道を示しておきます。
![]()
![]()
![]() より
より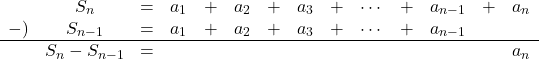
よって, ![]()
同様にして, ![]()
![]()
![]() より
より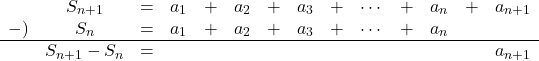
よって,![]()
以上になります。
漸化式で![]() が登場するときや, 漸化式に
が登場するときや, 漸化式に![]() が登場するときに使うと効果的です。使い方としては, 基本1つずらして引くことだけですので, 効果てきめんです。
が登場するときに使うと効果的です。使い方としては, 基本1つずらして引くことだけですので, 効果てきめんです。