こんにちは。今回は複素数について触れておきます。基本事項の確認だと思ってください。
複素数は回転を表す
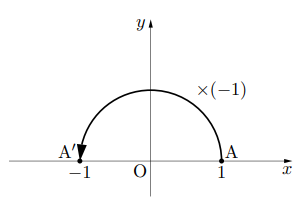
下の図のように, 1に![]() (負の数)をかけることを数直線上で180
(負の数)をかけることを数直線上で180![]() の回転とみる。すると下の図のように,
の回転とみる。すると下の図のように,
1が![]() 倍されることで180
倍されることで180![]() 回転して
回転して![]() になり, 再度
になり, 再度![]() (180
(180![]() )をかけるとで, 1に戻る。このように, 負の数をかけることは, 数直線上では180
)をかけるとで, 1に戻る。このように, 負の数をかけることは, 数直線上では180![]() の回転を意味する。
の回転を意味する。
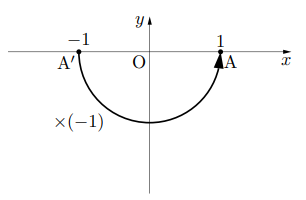
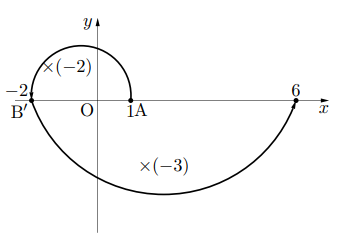
右の図は, 1に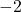 をかけた場合の様子を表しているが, この場合1は数直線上で原点を中心に, 180
をかけた場合の様子を表しているが, この場合1は数直線上で原点を中心に, 180 回転して, かつ2倍されている。このことは, 後述する複素数と話がつながってくるので, 覚えておこう。そして,
回転して, かつ2倍されている。このことは, 後述する複素数と話がつながってくるので, 覚えておこう。そして, 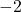 に
に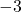 をかけると, 原点を中心に180
をかけると, 原点を中心に180 回転し, かつ3倍されて6となる。つまり,
回転し, かつ3倍されて6となる。つまり, 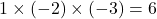 である。
である。
また, 同じ数字を2回かけて, 負の数になる数が数直線上には存在しないことがわかる。
![]() が存在していなったときに, いい考えを示した人がいました。それは,
が存在していなったときに, いい考えを示した人がいました。それは, ![]() をかけることが180
をかけることが180![]() の回転なら,
の回転なら, ![]() はその半分の90
はその半分の90![]() の回転としようと考えたのです。そうすると, どうでしょう。一旦数直線から離れることになります。数直線上にない数なので, 想像上の数(イマジナリーナンバー)の頭文字をとって
の回転としようと考えたのです。そうすると, どうでしょう。一旦数直線から離れることになります。数直線上にない数なので, 想像上の数(イマジナリーナンバー)の頭文字をとって![]() とすることにしました。これで実数軸と虚数軸が誕生したことになります。1回の回転が90
とすることにしました。これで実数軸と虚数軸が誕生したことになります。1回の回転が90![]() なので, 2回かけると180
なので, 2回かけると180![]() になります。つまり,
になります。つまり, ![]() 回転)ですから,
回転)ですから, ![]() 回転
回転![]() 回転
回転![]() 回転
回転![]() ))となるわけです。
))となるわけです。
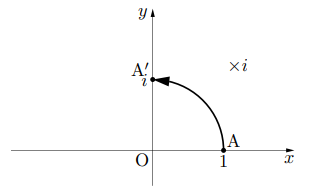
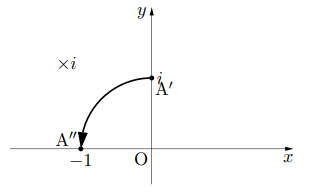
複素数の積の図形的意味
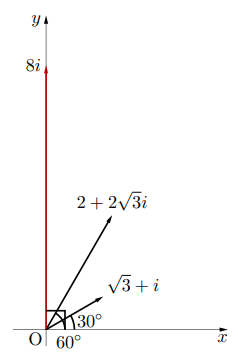
次に計算結果が分かりやすいように, 右図のような, 大きさ2, 偏角30 の複素数を考えると, その複素数は
の複素数を考えると, その複素数は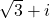 で表される。同様に大きさ4, 偏角60
で表される。同様に大きさ4, 偏角60 の複素数を考えると, その複素数は
の複素数を考えると, その複素数は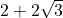 で表される。
で表される。
このとき, 2つの複素数の積は
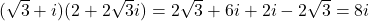
となる。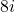 ということは虚数軸上にあり, 大きさ8, 偏角90
ということは虚数軸上にあり, 大きさ8, 偏角90 である。
である。
この大きさ8というのは, 初めの大きさ2と大きさ4の積で, 4倍されたことを意味し, 偏角90 というのは, 初めの偏角30
というのは, 初めの偏角30 と偏角60
と偏角60 の和になっている。言い換えれば原点を中心に, 偏角30
の和になっている。言い換えれば原点を中心に, 偏角30 に対して, 反時計回りに60
に対して, 反時計回りに60 回転したことを意味する。
回転したことを意味する。
このとき, 2つの複素数の積は
となる。
この大きさ8というのは, 初めの大きさ2と大きさ4の積で, 4倍されたことを意味し, 偏角90
これを極形式で表すと,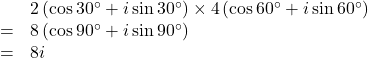
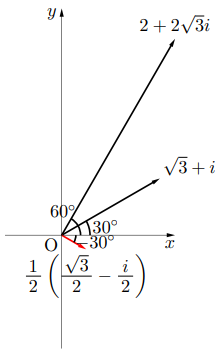
複素数の商の図形的意味
先と同じく, 大きさ2, 偏角30 の複素数を考えると, その複素数は
の複素数を考えると, その複素数は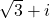 で表される。同様に大きさ4, 偏角60
で表される。同様に大きさ4, 偏角60 の複素数を考えると, その複素数は
の複素数を考えると, その複素数は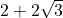 で表される。
で表される。
このとき, 2つの複素数の商は
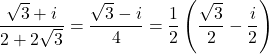
このとき, この計算結果の複素数の大きさは で偏角は
で偏角は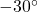 である。
である。
この大きさ というのは, 初めの大きさ2と大きさ4の商で,
というのは, 初めの大きさ2と大きさ4の商で,  倍されたことを意味し, 偏角
倍されたことを意味し, 偏角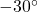 というのは, 初めの偏角30
というのは, 初めの偏角30 と偏角60
と偏角60 の差になっている。言い換えれば原点を中心に, 偏角30
の差になっている。言い換えれば原点を中心に, 偏角30 に対して, 時計回りに60
に対して, 時計回りに60 回転したことを意味している。
回転したことを意味している。
このとき, 2つの複素数の商は
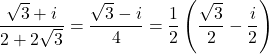
このとき, この計算結果の複素数の大きさは
この大きさ
これを極形式で表すと,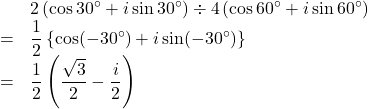
 数樂管理人のブログ
数樂管理人のブログ 

