こんにちは。今回は少々面倒な式の値も整式の除法を用いることで, 平易に求められるという事実を書いておきますね。例題を見ながらいきましょう。
代入値が有理数+無理数の場合の例題
【例】![]() のとき,
のとき, ![]() の値を求めよ。
の値を求めよ。
【解法】![]() から,
から, ![]() として, 両辺に乗すると,
として, 両辺に乗すると, ![]()
![]() より,
より, ![]() を得る。
を得る。
この式で, ![]() を割ると,
を割ると,
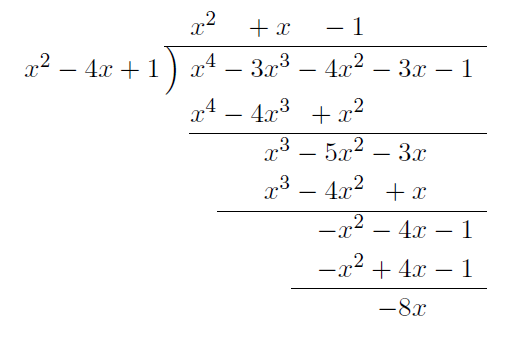
となり,
![]()
と変形でき, 下線部は0![]() から)なので, 求める式の値は
から)なので, 求める式の値は![]() の式の値を同値になる。
の式の値を同値になる。
よって, 求める値は, ![]() (答)
(答)
代入値が有理数+複素数の場合の例題
もう1つ![]() の値が複素数の場合の例題をやっておこう。
の値が複素数の場合の例題をやっておこう。
【例】 ![]() のとき,
のとき, ![]() の値を求めよ。
の値を求めよ。
【解法】先と同様に式変形を行っていく。![]() から,
から, ![]() として, 両辺に乗すると,
として, 両辺に乗すると, ![]()
![]() より,
より, ![]() を得る。
を得る。
この式で, ![]() を割ると,
を割ると,
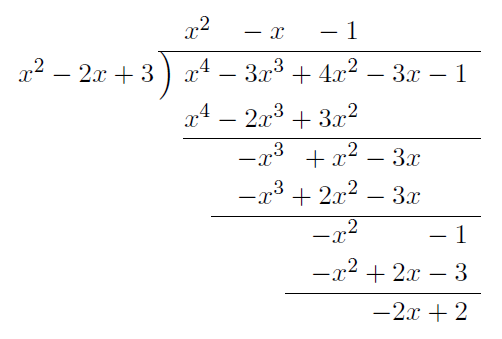
となり,
![]()
と変形でき, 下線部は0![]() から)なので, 求める式の値は
から)なので, 求める式の値は![]() の式の値を同値になる。
の式の値を同値になる。
よって, 求める値は, ![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 

