こんにちは。帰納法の解法を例題を解きながら見ていきましょう。
【例】![]() で定められる。数列
で定められる。数列![]() の一般項を予測して, それを数学的帰納法を用いて証明せよ。
の一般項を予測して, それを数学的帰納法を用いて証明せよ。
【方針】漸化式を使って, 数列![]() を予測し, 数学的帰納法を用いて, それがすべての
を予測し, 数学的帰納法を用いて, それがすべての![]() で成り立つことを示す。
で成り立つことを示す。
【解法】![]() のとき,
のとき, ![]()
![]()
![]()
以上より, 数列![]() の一般項は
の一般項は![]() と予測できる。
と予測できる。![]()
これを数学的帰納法で証明すると, ![]() のとき,
のとき, ![]() で成り立つ。
で成り立つ。![]() で
で![]() が成り立つとすると,
が成り立つとすると, ![]() が成り立ち,
が成り立ち, ![]() のとき,
のとき, 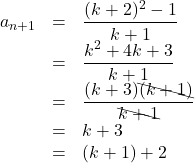
よって, ![]() のときも成り立つ。
のときも成り立つ。
したがって, 数学的帰納法により, すべての自然数において, ![]() であることが示された。
であることが示された。
つまり, 数列![]() の一般項は
の一般項は![]()
帰納法と漸化式
一般項を予測し, 予測した一般項を漸化式に代入して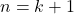 のとき成り立つことを示す。
のとき成り立つことを示す。
 数樂管理人のブログ
数樂管理人のブログ 


