高校数学：数列・等比数列の性質を用いた解法①

こんにちは。今回は等比数列の性質を用いた解法の紹介です。例題を解きながら書いておきます。それでは見ていきましょう。

等比数列の性質を知ろう

まず簡単な等比数列から見ていきます。
$1,\ 2,\ 4,\ \cdots 32,\ 64,\ 128,\ \cdots$
このとき, 等比数列の連続する3項には, 真ん中の数の2乗はその両隣の数の積になっているという決まりがあるんです。実際 $1, 2, 4$ では $2^2=1\times4$ , また, 32, 64, 128でも $64^2(4096)=32\times128(4096)$ になっています。
文字で置いて確認すると, 初項 $a$ , 公比 $r$ とすると,
$a,\ ar,\ ar^2,\ \cdots$
$(ar)^2=a\times ar^2$
となっています。
この性質を用いて問題を解いていきましょう。それでは例題です。
【例】数列 $2,\ x,\ 5x-12, \cdots$ が等比数列であるとき, $x$ の値を求めよ。
【解法】真ん中の数の2乗＝真ん中の数の両隣の数の積で解いていきます。
$x^2=2(5x-12)$
$x^2-10x+24=0$
$(x-4)(x-6)=0$
$x=4, 6\cdots$ (答)
ちなみに,
$x=4$ のとき, $2, 4, 8, \cdots$ 　公比2
$x=6$ んとき, $2, 6, 18, \cdots$ 　公比3

等比数列の性質

等比数列の連続する3項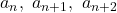 $a_{n},\ a_{n+1},\ a_{n+2}$ には,
$(a_{n+1})^2=a_n\times a_{n+2}$
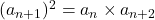
真ん中の数の2乗＝真ん中の両隣の数の積
が成り立つ。

別解として公比が等しいという解法があります。
$ar\div a=r,\ ar^2\div ar=r$ , つまり, $\dfrac{ar}{a}=\dfrac{ar^2}{ar}$ を用いた解法です。
$\dfrac{x}{2}=\dfrac{5x-12}{x}$
$x^2=10x-24$
$x^2-10x+24=0$
以下略(上と同じのため)

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル