こんにちは。今回は等差数列の性質を用いた基本的な問題の解法を書いておきます。例題を解きながら見ていきましょう。
等差数列の性質を知ろう
まず簡単な等差数列を見ていきましょう。![]()
このとき, 1, 2, 3の2はその両隣にある2数の平均になっています。つまり, ![]() です。
です。
16, 17, 18でも同様に, 17はその両隣にある2数の平均になっています。![]() です。
です。
これは言い換えると, 等差数列の連続する3項では, 真ん中の数の両隣の数の和が真ん中の数の2倍になっていることを意味します。
文字でおくとどうでしょう。
初項![]() , 公差
, 公差![]() の等差数列を第1項から書くと,
の等差数列を第1項から書くと, ![]()
確かに, ![]()
![]()
になっています。
そこで, 例題です。
【例】数列![]() が等差数列のとき,
が等差数列のとき, ![]() の値を求めなさい。
の値を求めなさい。
【解法】 真ん中の数の両隣の数の和が真ん中の数の2倍になるという決まりに従って解きます。![]()
![]()
![]()
![]()
![]() (答)
(答)
ちなみに![]() のとき,
のとき, ![]() 公差
公差![]()
![]() のとき,
のとき, ![]() 公差
公差![]()
になります。
このように, 等差数列の連続する3項の真ん中の数の両隣の数の和が真ん中の数の2倍になるということがつかめたら平易に解法に持っていけるでしょう。
等差数列の性質
等差数列の連続する3項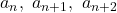 には,
には,
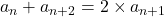
真ん中の両隣の数の和=真ん中の数の2倍
が成り立つ。
真ん中の両隣の数の和=真ん中の数の2倍
が成り立つ。
別解として, 等差数列なので, 公差が等しいとおいて解く解法があります。(こちらが好きな方はこちらをどうぞ)![]()
![]()
![]()
以下略(上と同じのため)
 数樂管理人のブログ
数樂管理人のブログ 

