こんにちは。今回はデータの分散と標準偏差の公式について書いておきます。
平均![]()
データ![]() の平均を
の平均を![]() とすると,
とすると, ![]()
偏差![]()
データ![]() の各数値と, データの平均
の各数値と, データの平均![]() との差。
との差。![]()
分散![]()
分散![]() はデータの散らばり度合いを表すもので, 上の偏差の2乗の平均をとったものです。したがって,
はデータの散らばり度合いを表すもので, 上の偏差の2乗の平均をとったものです。したがって, ![]()
このようにして分散は得られます。
また, この右辺を展開すると, 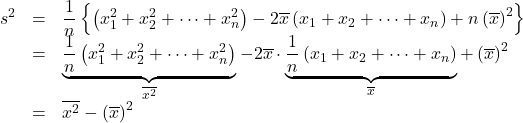
このように, 分散は![]() のデータの平均から
のデータの平均から![]() のデータの平均の2乗を引いても得られます。
のデータの平均の2乗を引いても得られます。
標準偏差![]()
標準偏差![]() は分散の正の平方根になります。したがって,
は分散の正の平方根になります。したがって, ![]()
または, ![]()
で得られます。
これらはデータの分野では頻出ですのでもれなく覚えておきたいですね。
符号決定
または,
または,
 数樂管理人のブログ
数樂管理人のブログ 

