こんにちは。今回は条件付き確率について書いておきます。例題を解きながら見ていきましょう。
条件付き確率とは
【条件付き確率とは】事象![]() が起こったとして, そのときに事象
が起こったとして, そのときに事象![]() が起こる確率のことを,
が起こる確率のことを, ![]() が起こったときに
が起こったときに![]() が起こる条件付き確率といいます。この条件付き確率は一般に
が起こる条件付き確率といいます。この条件付き確率は一般に![]()
で表されます。
つまり事象![]() が起こったという状況の中での確率なので, 分母には事象
が起こったという状況の中での確率なので, 分母には事象![]() の確率がきます。その中で事象
の確率がきます。その中で事象![]() が起こるので分子には事象
が起こるので分子には事象![]() (
(![]() かつ
かつ![]() )の確率がきます。したがって
)の確率がきます。したがって![]() という表現になります。このように条件付き確率では, 事象全体の確率ではなく, 事象全体の範囲が事象
という表現になります。このように条件付き確率では, 事象全体の確率ではなく, 事象全体の範囲が事象![]() だけに限られる場合の確率になります。
だけに限られる場合の確率になります。
事象Aが全事象になる
【例】袋の中に1から5までの自然数が1つずつ書かれ5個の赤玉と, 1から5までの自然数が1つずつ書かれた5個の白玉がある。この袋の中から玉を1個取り出したとき, 赤玉が出た。この玉に書かれている数が偶数である確率を求めなさい。
【解法】この場合, 事象![]() にあたるのが赤玉が出たという事象です。では赤玉が出る確率
にあたるのが赤玉が出たという事象です。では赤玉が出る確率![]() は10個の中の5個が赤玉なので,
は10個の中の5個が赤玉なので, ![]() 。事象
。事象![]() にあたるのが偶数であるという事象なので,
にあたるのが偶数であるという事象なので, ![]() という赤玉かつ偶数が出るという確率は10個の中に赤玉の2, 4の2個しかないので,
という赤玉かつ偶数が出るという確率は10個の中に赤玉の2, 4の2個しかないので, ![]() 。
。
よって, 求める条件付き確率![]() は,
は,
![]()
2017年のセンター試験から一部抜粋
【例】あたりが2本, はずれが2本の合計4本からなるくじがある。A, B, C の3人がこの順に1本ずつくじを引く。ただし, 1度引いたくじはもとに戻さない。
(1) A, B の少なくとも一方があたりのくじを引く事象![]() の確率は, 【
の確率は, 【 ![]() 】である。
】である。
(2) 次の【 ![]() 】,【
】,【 ![]() 】, 【
】, 【 ![]() 】 に当てはまるものを、下の0 ~ 5のうちから一つずつ選べ。ただし, 解答の順序は問わない。
】 に当てはまるものを、下の0 ~ 5のうちから一つずつ選べ。ただし, 解答の順序は問わない。
A, B, C の3人で2本のあたりのくじを引く事象![]() は, 3つの排反な事象【
は, 3つの排反な事象【 ![]() 】,【
】,【 ![]() 】,【
】,【 ![]() 】の和事象である。
】の和事象である。
0 A がはずれのくじを引く事象
1 A だけがはずれのくじを引く事象
2 B がはずれのくじを引く事象
3 B だけがはずれのくじを引く事象
4 C がはずれのくじを引く事象
5 C だけがはずれのくじを引く事象
また、その和事象の確率は 【 ![]() 】である。
】である。
(3) 事象 ![]() が起こったときの事象
が起こったときの事象![]() の起こる条件付き確率は, 【
の起こる条件付き確率は, 【 ![]() 】である。
】である。
【解法】
(1) 余事象を考える。 A, B の少なくとも一方があたりのくじを引くという事象![]() の余事象
の余事象![]() は, A, Bがともにはずれを引く事象なので,
は, A, Bがともにはずれを引く事象なので,
確率![]()
よって求める確率は, 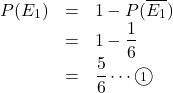
(2) 3人のうち2人が当たるということは1人だけはずれが出るということ。
したがって, A, Bが当たってCだけはずれる。A, Cが当たってBだけはずれる。B, Cが当たってAだけはずれる。という3つの事象の和事象になる。よって, ![]() 順不同
順不同
この和事象の確率は, 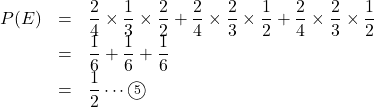
ちなみにこの上の確率を説明すると,
以下(Aのひく確率)![]() (Bのひく確率)
(Bのひく確率)![]() (Cのひく確率)の順で記しています。
(Cのひく確率)の順で記しています。![]() A, Bが当たりでCがはずれを引く確率(Cだけはずれ)。
A, Bが当たりでCがはずれを引く確率(Cだけはずれ)。 ![]() Aが当たりBがはずれを引いてCが当たる確率(Bだけはずれ)。
Aが当たりBがはずれを引いてCが当たる確率(Bだけはずれ)。![]() Aがはずれを引いてB, Cが当たる確率(Aだけはずれ)。
Aがはずれを引いてB, Cが当たる確率(Aだけはずれ)。
(3) 事象![]() (A, Bの少なくとも一方が当たった)が起こった中で, 事象
(A, Bの少なくとも一方が当たった)が起こった中で, 事象![]() (2人は当たりで1人だけはずれを引く)が起こる条件付き確率
(2人は当たりで1人だけはずれを引く)が起こる条件付き確率![]() は,
は, 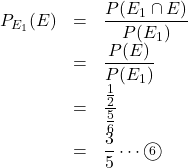
 数樂管理人のブログ
数樂管理人のブログ 

