こんにちは。今回は空間ベクトルで知っておくと便利な知識を活用しようというお話です。例題を解きながら見ていきましょう。
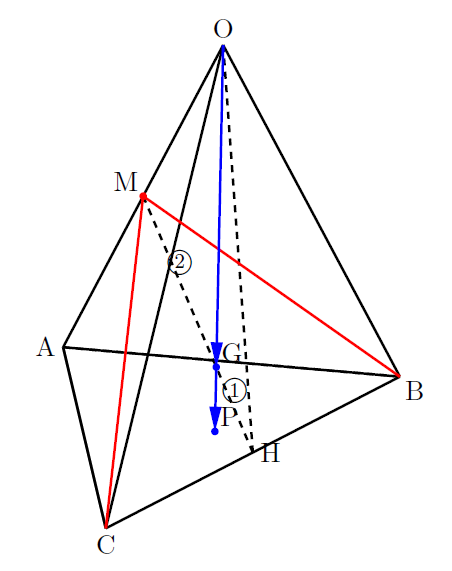
【例】四面体OABCにおいて, 辺OAの中点をM, ![]() の重心をGとし, 直線OGと平面ABCの交点をPとする。
の重心をGとし, 直線OGと平面ABCの交点をPとする。![]() ,
, ![]() ,
, ![]() とするとき, 次の問いに答えなさい。
とするとき, 次の問いに答えなさい。
(1) ![]() を
を![]() ,
, ![]() ,
, ![]() を用いて表せ。
を用いて表せ。
(2) ![]() を
を ![]() ,
, ![]() ,
, ![]() を用いて表せ。
を用いて表せ。
【解法】
(1)線分BCの中点をHとして, 分点の公式を用いると,
![]()
また, ![]()
![]()
であるから, ![]() より,
より, 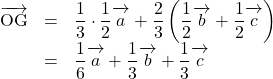
よって,![]()
ちょっと一工夫すると
Gは![]() の重心なので,
の重心なので,![]()
![]() なので,
なので,![]()
よって,![]()
(2) ![]() なので,
なので, ![]()
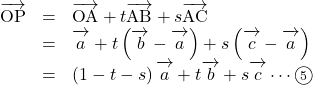
![]() と
と![]() の係数を比較すると,
の係数を比較すると, ![]()
![]()
これから, ![]()
したがって, ![]()
ちょっと一工夫すると
![]() なので,
なので,![]()
点Pは平面ABC上にあるから,![]()
![]() より,
より, ![]()
したがって,![]()
s+t+u=1をうまく使おう
点Pが平面上にあるときは, ![]() などとおいて,
などとおいて, ![]() からベクトルの係数の和を1とする方程式をつくり,
からベクトルの係数の和を1とする方程式をつくり, ![]() の値を求めると手際よく解ける。
の値を求めると手際よく解ける。
 数樂管理人のブログ
数樂管理人のブログ