高校数学：等差数列と等比数列の性質の融合問題

2021年11月14日2022年5月2日

SHARE

こんにちは。今回は等差数列と等比数列の性質の融合問題です。まずはそれぞれの性質をおさらいしておきましょう。

等差数列と等比数列の性質のおさらい

等差数列の性質のおさらい。

等差数列の性質

3つの数, 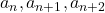$a_n, a_{n+1}, a_{n+2}$ がこの順で等差数列をなすとき,
$2a_{n+1}=a_n+a_{n+2}$
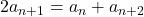
が成り立つ。

等比数列の性質のおさらい。

等比数列の性質

3つの数, 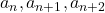$a_n, a_{n+1}, a_{n+2}$ がこの順で等比数列をなすとき,
$\left(a_{n+1}\right)^2=a_n\cdot a_{n+2}$
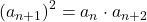
が成り立つ。

これらを使う問題がこちら

例題(融合問題)

【例】 $ab\neq0$ とする。3つの数 $8, a, b$ がこの順に等差数列をなし, $a, b, 36$ がこの順に等比数列をなすという。 $a, b$ の値を求めよ。
【解法】等差数列の性質より,
$2a=8+b\cdots\maru1$
等比数列の性質より,
$b^2=36a\cdots\maru2$
$\maru2$ は次のように書ける。
$b^2=18\cdot2a\cdots\maru2 '$
$\maru2 '$ に $\maru1$ を代入すると,
$b^2=18(8+b)$
$b^2-18b-144=0$
$(b-24)(b+6)=0$
$b=24, -6$
$b=24$ のとき, $a=16$
$b=-6$ のとき, $a=1$
よって, 求める $a, b$ の値は,
$(a, b)=(16, 24), (1, -6)$

コメントを残すコメントをキャンセル

前の記事

中学数学：学校のテスト・投影図と立体の問題

次の記事

森岡毅さんから学ぶ(初耳学まとめ2021.11.14放送)