今回は複雑な数列の和を求めてみましょう。例題を解きながら見ていきましょう。
【例題】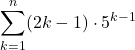 の値を求めよ。
の値を求めよ。
【解法】
求める値を![]() とすると,
とすると, ![]()
これを5倍する(公比を両辺にかける)と![]()
![]() を行うと,
を行うと, 
![]() より
より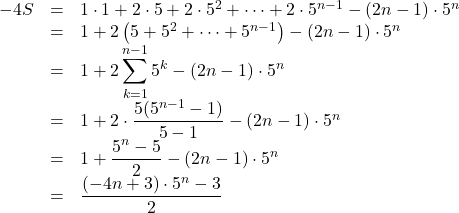
両辺![]() で割って,
で割って, ![]() (答)
(答)
この問題を解いてみて, 結果が面白いことに気づきました。
結果から考察すると, ![]() が8の倍数になるんですよ。時間のある人は数学的帰納法で証明してみてください。これだから数学は楽しい。解答はこちら。
が8の倍数になるんですよ。時間のある人は数学的帰納法で証明してみてください。これだから数学は楽しい。解答はこちら。
複雑な数列の和の求め方
今回は複雑な数列の和を求めてみましょう。例題を解きながら見ていきましょう。
【例題】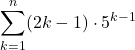 の値を求めよ。
の値を求めよ。
【解法】
求める値を![]() とすると,
とすると, ![]()
これを5倍する(公比を両辺にかける)と![]()
![]() を行うと,
を行うと, 
![]() より
より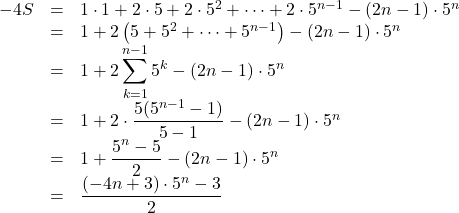
両辺![]() で割って,
で割って, ![]() (答)
(答)
この問題を解いてみて, 結果が面白いことに気づきました。
結果から考察すると, ![]() が8の倍数になるんですよ。時間のある人は数学的帰納法で証明してみてください。これだから数学は楽しい。解答はこちら。
が8の倍数になるんですよ。時間のある人は数学的帰納法で証明してみてください。これだから数学は楽しい。解答はこちら。