こんにちは。今回は複雑な数列の和から得られた結果が本当に8の倍数になるのか考察してみようと思います。
【問題】自然数を![]() とするとき,
とするとき, ![]() が8の倍数になることを数学的帰納法を用いて表せ。
が8の倍数になることを数学的帰納法を用いて表せ。
【解答】
![]() のとき,
のとき, ![]()
で成り立つ。![]() のとき,
のとき, ![]() (
(![]() は自然数)
は自然数)
が成り立つと仮定すると, ![]() のとき,
のとき, 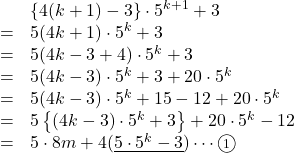
ここで, ![]() の下線部は奇数
の下線部は奇数![]() 奇数なので偶数であるから,
奇数なので偶数であるから, ![]() (
(![]() は自然数)とおける。
は自然数)とおける。
よって, ![]() は,
は, ![]()
となり, これは8の倍数である。
したがって, ![]() において成り立つ事が言える。
において成り立つ事が言える。
ゆえに, すべての自然数![]() について成り立つ事が言える。
について成り立つ事が言える。
 数樂管理人のブログ
数樂管理人のブログ 


