こんにちは。今回は数学的帰納法の問題をやっていてこれは手品か?と思ったのがあったのでご紹介も兼ねてやってみようと思います。
【例題】![]() は自然数とする。数学的帰納法を用いて,
は自然数とする。数学的帰納法を用いて, ![]()
が成り立つことを証明せよ。
【解法】
この等式を(A)とすると, ![]() のとき,
のとき,
左辺 : ![]() , 右辺 :
, 右辺 : ![]()
で成り立つ。![]() のとき, この等式
のとき, この等式
![]()
が成り立つとすると, ![]() のとき
のとき
(A)の(左辺)を考えると, 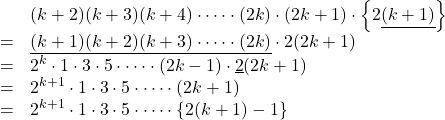
よって, ![]() のときも成り立つ。
のときも成り立つ。
以上より, すべての自然数![]() について(A)が成り立つ。
について(A)が成り立つ。
まず上の1行目の下線部の![]() は先頭に移動する。すると2行目の下線部の式は, 問題の等式の右辺と置き換えができて, 3行の下線部の2は先頭の
は先頭に移動する。すると2行目の下線部の式は, 問題の等式の右辺と置き換えができて, 3行の下線部の2は先頭の![]() とくっつき
とくっつき![]() に変身するという手品みたいな技。こんな風に数学にも手品?のような技があったのでした。
に変身するという手品みたいな技。こんな風に数学にも手品?のような技があったのでした。
 数樂管理人のブログ
数樂管理人のブログ 

