こんにちは。今回は高1の整数のところで出てくる最大公約数と最小公倍数の性質の紹介。
2つの整数![]() の最大公約数を
の最大公約数を![]() , 最小公倍数を
, 最小公倍数を![]() とする。
とする。![]() (
(![]() は互いに素)であるとき, 次の式が成り立つ。
は互いに素)であるとき, 次の式が成り立つ。![]()
![]()
![]()
![]()
![]() は,
は, ![]() から
から![]()
と書けるので, ![]() が導ける。
が導ける。
【例題】最大公約数が25, 最小公倍数が900である自然数![]() の組をすべて求めよ。
の組をすべて求めよ。
【解法】求める2数![]() を
を![]() (
(![]() は互いに素)とおく。ただし,
は互いに素)とおく。ただし, ![]() とする。
とする。
このとき最小公倍数は![]() と表されるので,
と表されるので, ![]()
![]()
となる。![]() は互いに素で
は互いに素で![]() であることを考えると,
であることを考えると, ![]()
よって求める自然数![]() の組は
の組は![]()
最大公約数G, 最小公倍数L
2つの整数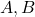 の最大公約数を
の最大公約数を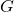 , 最小公倍数を
, 最小公倍数を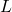 とする。
とする。
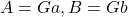 (
(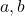 は互いに素)であるとき, 次の式が成り立つ。
は互いに素)であるとき, 次の式が成り立つ。

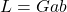

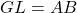
 数樂管理人のブログ
数樂管理人のブログ 


