こんにちは。今回は積分で使う技を紹介します。使えると計算量を減らすことができるので, 覚えておきましょう。
![]() を定数とすると, 積分区間が
を定数とすると, 積分区間が![]() から
から![]() という具合に絶対値が同じになる正負の積分区間において次の事が言える。
という具合に絶対値が同じになる正負の積分区間において次の事が言える。
以下![]() は0以上の整数とすると,
は0以上の整数とすると, ![]() 奇数乗は0
奇数乗は0![]() 偶数乗は2倍
偶数乗は2倍
【証明1】![]() の証明
の証明![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int^{a}_{-a}x^{2n+1}\,dx&=&\left[\dfrac{x^{2n+2}}{2n+2}\right]^{a}_{-a}\\&=&\dfrac{a^{2n+2}}{2n+2}-\dfrac{(-a)^{2n+2}}{2n+2}\cdots\maru1\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-8efdc1f0d5511599a878e2268c463057_l3.png)
![]() の指数部
の指数部![]() は偶数なので,
は偶数なので, ![]() と書ける。
と書ける。
したがって, ![]() は
は![]()
つまり, ![]()
【証明2】![]() の証明
の証明![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int^{a}_{-a}x^{2n}\,dx&=&\left[\dfrac{x^{2n+1}}{2n+1}\right]^{a}_{-a}\\&=&\dfrac{a^{2n+1}}{2n+1}-\dfrac{(-a)^{2n+1}}{2n+1}\cdots\maru2\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-17531b1ab466e9930681b62930b82c9b_l3.png)
![]() の指数部
の指数部![]() は奇数なので,
は奇数なので, ![]() と書ける。
と書ける。
したがって, ![]() は
は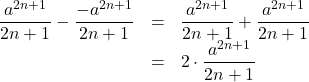
よって, ![]()
ここで, ![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int^{a}_{0}x^{2n}\,dx&=&\left[\dfrac{x^{2n+1}}{2n+1}\right]^{a}_{0}\\&=&\dfrac{a^{2n+1}}{2n+1}\cdots\maru4\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-89f3d9c36520a0543d1e7667628258ec_l3.png)
![]() より,
より, ![]()
【例題】次の定積分を求めよ。![]()
![]()
![]()
![]() (奇関数は0)
(奇関数は0)![]()
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int^{3}_{-3}x^2\,dx&=&2\displaystyle\int^{3}_{0}x^2\,dx\\&=&2\left[\dfrac13x^3\right]^{3}_{0}\\&=&18\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-7424f48b183add3a483dfa565a371619_l3.png)
(偶関数は2倍)![]()
![Rendered by QuickLaTeX.com \begin{array}{lll} \displaystyle\int^{3}_{-3}(x^3+2x^2+x+1)\,dx&=&2\displaystyle\int^{3}_{0}(2x^2+1)\,dx\\&=&2\left[\dfrac23x^3+x\right]^{3}_{0}\\&=&42\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-66f168c9e70e53306e1b57ef11393cc6_l3.png)
このように奇数乗の単項式(奇関数)は0になるので, 省いて計算できます。
 数樂管理人のブログ
数樂管理人のブログ 

