こんにちは。今回は座標平面上の三角形の面積を求める公式を証明しましょう。
座標平面上の三角形の面積の公式
座標平面上の3点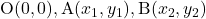 を頂点とする
を頂点とする
三角形の面積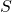 を求める公式は
を求める公式は
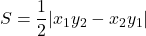
絶対値の中はA, Bの座標をたすき掛けしたものの差になる。
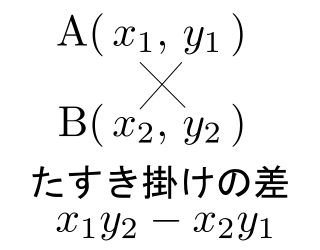
三角形の面積
絶対値の中はA, Bの座標をたすき掛けしたものの差になる。
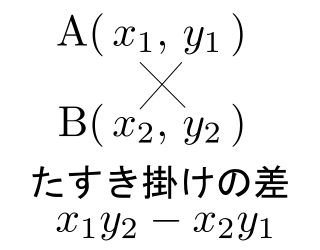
【方針】座標平面上の3点![]() を頂点とする三角形において,
を頂点とする三角形において, ![]() のとき直線ABの式を求め, その直線と原点の距離を求め三角形の面積を求めることにする。
のとき直線ABの式を求め, その直線と原点の距離を求め三角形の面積を求めることにする。![]() のときは, 底辺が
のときは, 底辺が![]() 軸に垂直になるため容易に求められる。
軸に垂直になるため容易に求められる。
【証明】
( i )![]() のとき, 直線ABの式は,
のとき, 直線ABの式は, ![]()
両辺に![]() をかけて,
をかけて, ![]() の形に変形すると,
の形に変形すると, ![]()
したがって, この直線と原点Oの距離![]() は,
は, ![]()
ここで, ![]() の分母は, 2点A, Bの距離を表す式
の分母は, 2点A, Bの距離を表す式![]() になっていることに着目し,
になっていることに着目し,
ABを底辺, 高さを![]() として, 三角形の面積
として, 三角形の面積![]() を求めると,
を求めると, 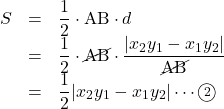
![]() の絶対値の中は順番を入れ替えても問題はないので,
の絶対値の中は順番を入れ替えても問題はないので, ![]()
となる。
( ii )![]() のとき,
のとき, ![]() ,
, ![]() から
から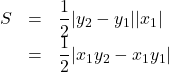
となり, これは![]() に含めることができる。
に含めることができる。
( i ), ( ii )より, ![]()
【例題】3点(0, 0), (2, 6), (4, 1)を頂点とする三角形の面積を求めよ。
![]()
![]() (答)
(答)
どの頂点も原点にない場合はどれか1つの頂点に着目し, それを原点に平行移動させて面積を求めます。この場合, 残りの2つの頂点も同じ量だけ平行移動させます。次の例題を見てみましょう。
【例題】3点![]() を頂点とする三角形の面積を求めよ。
を頂点とする三角形の面積を求めよ。
【解法】移動量の少ないAを原点に移すとして, 3点A, B, Cの![]() 座標を
座標を![]() ,
, ![]() 座標を
座標を![]() すると,
すると, ![]()
![]()
![]()
三角形![]() の面積を求めることは, 三角形
の面積を求めることは, 三角形![]() の面積を求めることと同じなので,
の面積を求めることと同じなので,
これに公式を適用し, ![]()
![]() (答)
(答)
最後に例題をやってみましょう。
【例題】3点![]() を頂点とする三角形の面積を求めよ。
を頂点とする三角形の面積を求めよ。
点![]() を原点に移すとして
を原点に移すとして![]()
よって求める面積は, ![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 

