こんにちは。今回は積分の基本公式を書いておきます。以下![]() は積分定数です。
は積分定数です。
定義として![]() とすると,
とすると, ![]()
があります。
基本公式![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
※![]() の積分は置換積分に書いてます。
の積分は置換積分に書いてます。
次の積分も公式として覚えておいてもいいでしょう。詳しくは部分積分で行います。![]()
![]()
![]() 積分するものが因数分解の形で書かれている場合は, 展開して積分すると大丈夫な場合がある。
積分するものが因数分解の形で書かれている場合は, 展開して積分すると大丈夫な場合がある。
【例】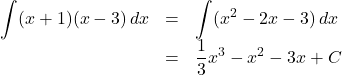
![]()
![]() の積分は
の積分は![]() に直して積分するとよい。
に直して積分するとよい。
【例】![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int \sqrt[3]{x^2} \,dx&=&\displaystyle\int x^{\frac23} \,dx\\&=&\dfrac35 x^{\frac53}+C\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-9cd21d9dc68f610b859ef6bdf756faec_l3.png)
![]()
![]() の積分は
の積分は![]() と変形して積分するとよい。
と変形して積分するとよい。
【例】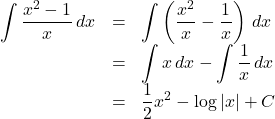
![]() ,
, ![]() ,
, ![]() は, 2倍角の公式を用いて,
は, 2倍角の公式を用いて, ![]() ,
, ![]() を用いた式に書き換えて積分するのが定石です。
を用いた式に書き換えて積分するのが定石です。![]()
![]() から,
から, ![]()
![]()
![]() から,
から, ![]()
![]()
![]() から,
から, ![]()
などを用いる。
【例】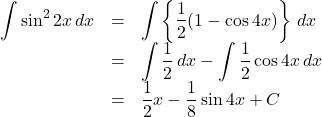
 数樂管理人のブログ
数樂管理人のブログ 

