こんにちは。今回は数IIIの積分で部分積分法について少し書いておきます。以下![]() は積分定数です。
は積分定数です。
部分積分法の公式は以下になります。![]() を積分
を積分![]() を微分
を微分![]() を積分
を積分![]()
上の公式で問題になってくるのが, ![]() の決め方ですが,
の決め方ですが, ![]() には微分しやすいもの, 特に微分すると次数が下がるものを選ぶといいでしょう。
には微分しやすいもの, 特に微分すると次数が下がるものを選ぶといいでしょう。![]() には積分しても変わらないもの選ぶか, 積分するとより簡単になるものを選ぶといいでしょう。
には積分しても変わらないもの選ぶか, 積分するとより簡単になるものを選ぶといいでしょう。
また, ![]() の積分などで使う次の部分積分法の技は知っておくといいでしょう。
の積分などで使う次の部分積分法の技は知っておくといいでしょう。![]()
これは, ![]() を
を![]() として, 1を積分して,
として, 1を積分して, ![]() を微分するという部分積分法のテクニックです。
を微分するという部分積分法のテクニックです。
【例】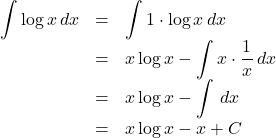
![]() では,
では, ![]() を
を![]() 積分する側)にとって,
積分する側)にとって, ![]() は
は![]() 微分する側)にとるとうまくいくことが多い。
微分する側)にとるとうまくいくことが多い。
【例】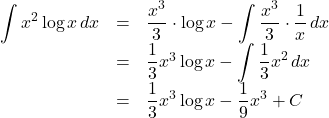
![]() では,
では, ![]() を
を![]() 微分する側)にとって,
微分する側)にとって, ![]() を
を![]() 積分する側)にとるとうまくいくことが多い。
積分する側)にとるとうまくいくことが多い。
【例】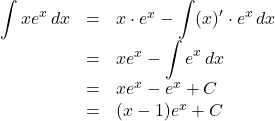
三角関数の![]() や
や![]() では2回微分すると, 同じ
では2回微分すると, 同じ![]() や
や![]() が現れることはご存知かと思います。この性質は積分に関しても同じです。したがって,
が現れることはご存知かと思います。この性質は積分に関しても同じです。したがって, ![]() や
や![]() では,
では, ![]() を
を![]() (微分)か
(微分)か![]() (積分)かどちらが楽になるかで判断すればよい。
(積分)かどちらが楽になるかで判断すればよい。
【例】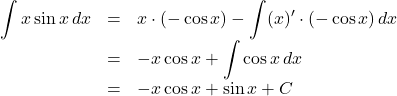
【例】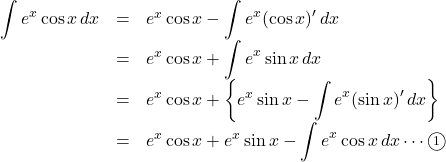
![]() から,
から, ![]()
となり, 右辺の![]() を左辺に移項して, 計算すると,
を左辺に移項して, 計算すると, ![]()
であるから, ![]()
となる。
 数樂管理人のブログ
数樂管理人のブログ 
