TikZ：高校数学：数III積分・定積分と面積

2022年5月21日2022年5月26日

SHARE

今回は, 数IIIの定積分と面積について書いておきます。一部数II内容と被るところがありますがご了承ください。

基本は数IIで学んだことと同じ

【パターン1】
以下の図形の面積 $S$ は次の定積分で与えられる。
$S=\displaystyle\int^b_a f(x)\,dx$

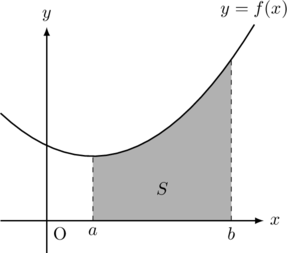
【パターン2】
以下の図形の面積 $S$ は次の定積分で与えられる。
$S=-\displaystyle\int^b_a f(x)\,dx$

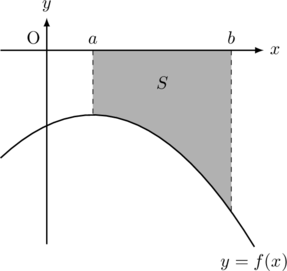
【パターン3】
以下の図形の面積 $S$ は次の定積分で与えられる。
$S=\displaystyle\int^b_a\left\{ f(x)-g(x)\right\}\,dx$

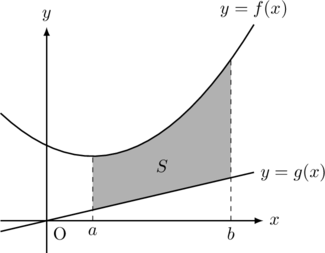
【パターン4】
以下の図形の面積 $S$ は次の定積分で与えられる。
$S=\displaystyle\int^b_a\left\{ g(x)-f(x)\right\}\,dx$

上の基本でx,yを入れ換えて考えると

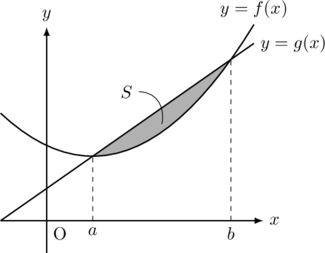
【パターン5】
以下の図形の面積 $S$ は次の定積分で与えられる。
$S=\displaystyle\int^b_a f(y)\,dy$

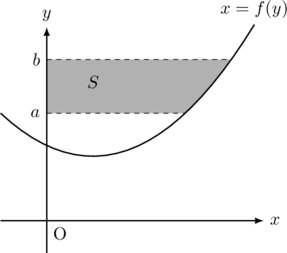
【パターン6】
以下の図形の面積 $S$ は次の定積分で与えられる。
$S=\displaystyle\int^b_a\left\{ f(y)-g(y)\right\}\,dy$

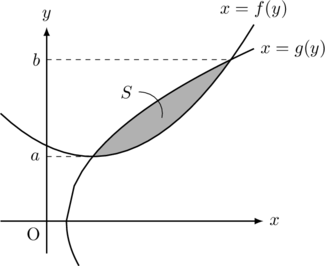
※考え方は【パターン4】と同じ。ただ, 見方としては, 関数が $x=$ ～で定義されているので, $x$ 軸の正の方向に見て, 右側にあるグラフ $(x=f(y))$ から, 左側にあるグラフ $(x=g(y))$ を引いて積分することに注意する。

関連記事

2022年5月22日TikZ：高校数学：積分・定積分と面積(なぜ積分で面積が求まるのか)

コメントを残すコメントをキャンセル

前の記事

TikZ：高校数学：積分・定積分と面積

次の記事

TikZ：高校数学：数III積分・定積分と体積(なぜ体積が求ま…