こんにちは。今回は定積分と体積について書いておきます。
以下のように![]() 軸上の点
軸上の点![]() を通り,
を通り, ![]() 軸に垂直な平面で切った立体がある。
軸に垂直な平面で切った立体がある。![]() として,
として, ![]() 軸上の点
軸上の点![]() を通り垂直な平面でこの立体を切ったときの断面積を
を通り垂直な平面でこの立体を切ったときの断面積を![]() とする。また, 区間[
とする。また, 区間[![]() ]の間の立体の体積を
]の間の立体の体積を![]() とする。
とする。
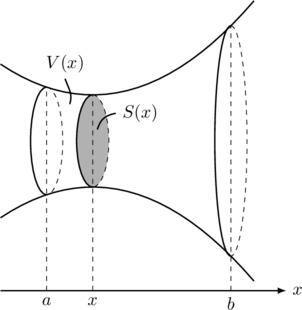
以下, 下図参照ください。
で表され,
とできる。
ここで,
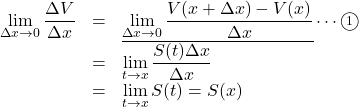
となり,
したがって,
一般に積分区間は
すなわち,
となる。
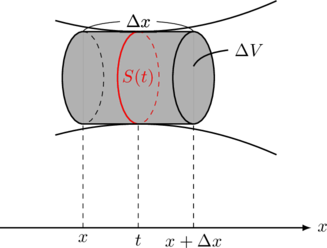
定積分と体積
![]() 軸に垂直な平面による断面積が
軸に垂直な平面による断面積が![]() である立体の体積
である立体の体積![]() は, 立体の区間を
は, 立体の区間を![]() とすると,
とすると, ![]()
 TikZ:高校数学:数III積分・x軸, y軸についての回転体の体積
TikZ:高校数学:数III積分・x軸, y軸についての回転体の体積
 TikZ:高校数学:数III積分・関数で囲まれた回転体の体積
TikZ:高校数学:数III積分・関数で囲まれた回転体の体積 数樂管理人のブログ
数樂管理人のブログ 
