こんにちは。今回はグラフを回転させてできる回転体の体積について書いておきます。
以下の図![]() で,
で, ![]() とする。曲線
とする。曲線![]() ,
, ![]() 軸, および2直線
軸, および2直線![]() で囲まれた図形を
で囲まれた図形を![]() 軸の回りに1回転してできる立体の体積を
軸の回りに1回転してできる立体の体積を![]() とする。
とする。
いま, 区間![]() で,
で, ![]() 軸上の点
軸上の点![]() を通り,
を通り, ![]() 軸に垂直な平面でこの回転体を切ったとき, 断面の円の半径はちょうど
軸に垂直な平面でこの回転体を切ったとき, 断面の円の半径はちょうど![]() になる。したがって, この位置における断面積
になる。したがって, この位置における断面積![]() は,
は, ![]()
となる。ゆえに, ![]() 軸について1回転させた立体の体積
軸について1回転させた立体の体積![]() は
は![]()
![]()
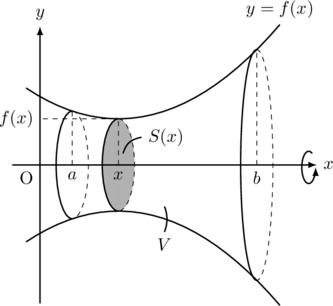
x軸について回転
曲線![]() ,
, ![]() 軸, および2直線
軸, および2直線![]() で囲まれた図形を
で囲まれた図形を![]() 軸について1回転させた立体の体積
軸について1回転させた立体の体積![]() は
は![]()
![]()
で与えられる。
![]() 軸について回転させる場合は, 上の
軸について回転させる場合は, 上の![]() 軸について回転させた場合の
軸について回転させた場合の![]() と
と![]() を入れ換えたものになる。
を入れ換えたものになる。
以下の図![]() で,
で, ![]() とする。曲線
とする。曲線![]() ,
, ![]() 軸, および2直線
軸, および2直線![]() で囲まれた図形を
で囲まれた図形を![]() 軸の回りに1回転してできる立体の体積を
軸の回りに1回転してできる立体の体積を![]() とする。
とする。
いま, 区間![]() で,
で, ![]() 軸上の点
軸上の点![]() を通り,
を通り, ![]() 軸に垂直な平面でこの回転体を切ったとき, 断面の円の半径はちょうど
軸に垂直な平面でこの回転体を切ったとき, 断面の円の半径はちょうど![]() になる。したがって, この位置における断面積
になる。したがって, この位置における断面積![]() は,
は, ![]()
となる。ゆえに, ![]() 軸について1回転させた立体の体積
軸について1回転させた立体の体積![]() は
は![]()
![]()
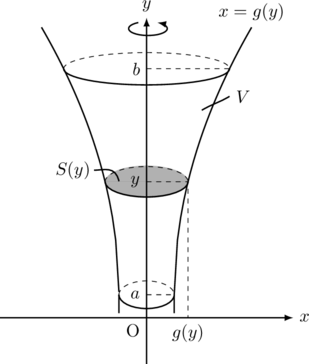
y軸について回転
曲線![]() ,
, ![]() 軸, および2直線
軸, および2直線![]() で囲まれた図形を
で囲まれた図形を![]() 軸について1回転させた立体の体積
軸について1回転させた立体の体積![]() は
は![]()
![]()
で与えられる。
 TikZ:高校数学:数III積分・定積分と体積(なぜ体積が求まるのか)
TikZ:高校数学:数III積分・定積分と体積(なぜ体積が求まるのか)
 TikZ:高校数学:数III積分・関数で囲まれた回転体の体積
TikZ:高校数学:数III積分・関数で囲まれた回転体の体積 数樂管理人のブログ
数樂管理人のブログ 
