こんにちは。今回は関数で囲まれた図形を![]() 軸や
軸や![]() 軸について回転させてできる立体の体積について書いておきます。
軸について回転させてできる立体の体積について書いておきます。
![]() のとき, 2曲線
のとき, 2曲線![]() ,
, ![]() , および2直線
, および2直線![]() ,
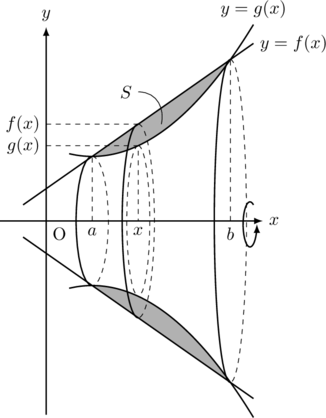
, ![]() で囲まれた図形を
で囲まれた図形を![]() 軸について1回転させてできる回転体の体積を
軸について1回転させてできる回転体の体積を![]() とすると, 立体の断面積
とすると, 立体の断面積![]() は図から,
は図から, ![]()
で与えられることから, ![]()
この式を注意してみると, この式は![]() の回転体の体積から,
の回転体の体積から, ![]() の回転体の体積を引いたものになっていることが分かる。
の回転体の体積を引いたものになっていることが分かる。
![]() 軸について回転させる場合は,
軸について回転させる場合は, ![]() 軸について回転させる場合の過程において,
軸について回転させる場合の過程において, ![]() を入れ換えればよい。したがって, 以下のようになる。
を入れ換えればよい。したがって, 以下のようになる。![]() のとき, 2曲線
のとき, 2曲線![]() ,
, ![]() , および2直線
, および2直線![]() ,
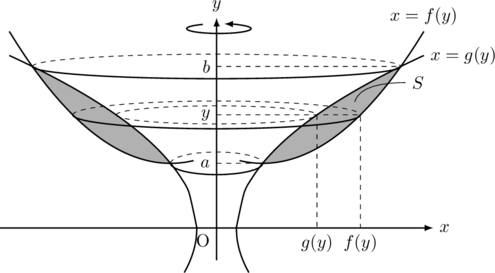
, ![]() で囲まれた図形を
で囲まれた図形を![]() 軸について1回転させてできる回転体の体積を
軸について1回転させてできる回転体の体積を![]() とすると, 立体の断面積
とすると, 立体の断面積![]() は図から,
は図から, ![]()
で与えられることから, ![]()
この式を注意してみると, この式は![]() の回転体の体積から,
の回転体の体積から, ![]() の回転体の体積を引いたものになっていることが分かる。
の回転体の体積を引いたものになっていることが分かる。
 TikZ:高校数学:数III積分・x軸, y軸についての回転体の体積
TikZ:高校数学:数III積分・x軸, y軸についての回転体の体積
 TikZ:高校数学:数III積分・定積分と体積(なぜ体積が求まるのか)
TikZ:高校数学:数III積分・定積分と体積(なぜ体積が求まるのか) 数樂管理人のブログ
数樂管理人のブログ 

