こんにちは。今回は区分求積法について書いておきます。
関数![]() が
が![]() において常に
において常に![]() であるとき,
であるとき, ![]() のグラフと
のグラフと![]() 軸, および2直線
軸, および2直線![]() で囲まれた面積を
で囲まれた面積を![]() とする。
とする。
図のように, 区間![]() を
を![]() 等分して, 左から順に,
等分して, 左から順に, ![]() とし, 分割の幅を
とし, 分割の幅を![]() とする。このとき, 図にできた
とする。このとき, 図にできた![]() 個の長方形の面積の和
個の長方形の面積の和![]() は,
は, 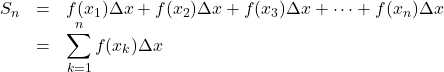
ただし, ![]() とする。
とする。
と表される。この式において, ![]() が十分大きいとき, その値は
が十分大きいとき, その値は![]() の値に近づき,
の値に近づき, ![]() は
は![]() において,
において, ![]() とした極限値であると考えてもよい。
とした極限値であると考えてもよい。
また, 面積![]() は区間
は区間![]() における関数
における関数![]() の定積分として与えられるから,
の定積分として与えられるから, 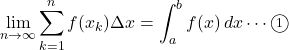
ただし, ![]() ,
, ![]()
が成り立つ。
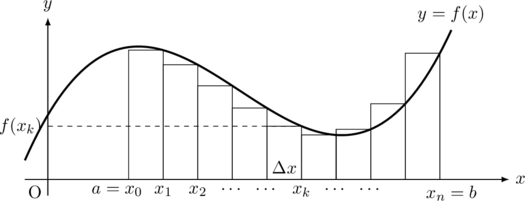
このように区間を分割して, その区間の面積を長方形の面積の和(数列の和)の極限として求める方法を, 区分求積法という。
また, この区分求積法において, 長方形の縦の長さは
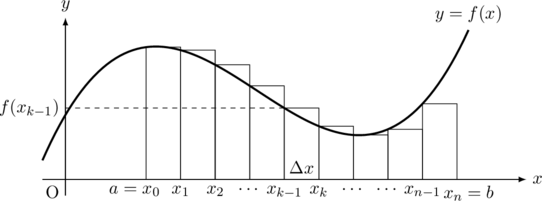
この場合の関係式は,
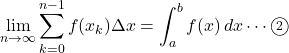
ただし,
となる。
上の![]() の式において,
の式において, ![]() ,
, ![]() とすると,
とすると, ![]()
![]() となるので,
となるので,
次式が得られる。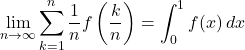
これを用いて, 数列の和の極限を, 定積分を用いて求められる場合がある。
ちなみに![]() 式の場合だと,
式の場合だと, 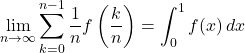
となる。
【例】次の極限を求めよ。
(1) 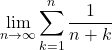
(2) ![]()
【解答例】
(1)![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{n\to\infty}\displaystyle\sum^{n}_{k=1}\dfrac{1}{n+k}&=&\displaystyle\lim_{n\to\infty}\displaystyle\sum^{n}_{k=1}\dfrac1n\cdot\dfrac{1}{1+\dfrac{k}{n}}\\&=&\displaystyle\int^1_0\dfrac{dx}{x+1}\,dx\\&=&\left[\log(1+x)\right]^1_0\\&=&\log2\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-b3079df0bad74cf0b8eef7707a4d5749_l3.png)
(2)![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{n\to\infty}\dfrac1n\displaystyle\sum^n_{k=1}\cos\dfrac{k\pi}{2n}&=&\displaystyle\lim_{n\to\infty}\dfrac1n\displaystyle\sum^n_{k=1}\cos\dfrac{\pi}{2}\cdot\dfrac{k}{n}\\&=&\displaystyle\int^1_0\cos\dfrac{\pi}{2}x\, dx\\&=&\left[\dfrac{2}{\pi}\sin\dfrac{\pi}{2}x\right]^1_0\\&=&\dfrac{2}{\pi}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-c8ccca99e7f6294acbcb03770da2ebdb_l3.png)
 数樂管理人のブログ
数樂管理人のブログ 

