こんにちは。三角関数で出てくる三角関数の積を和に直す公式です。それの紹介と導出です。
積和の公式とは次の3つです。
積和の公式
積和の公式![]()
![]()
![]()
![]()
![]()
![]()
今回はこの3つの公式を導いていきます。
用意するものは![]() と
と![]() の加法定理です。
の加法定理です。![]() の加法定理
の加法定理![]()
![]()
![]() の加法定理
の加法定理![]()
![]()
先ず![]() の公式は,
の公式は, ![]() の加法定理
の加法定理![]() と
と![]() を加えます。
を加えます。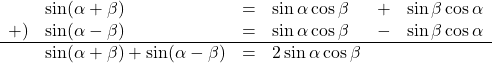
よって, ![]()
次に![]() の公式は,
の公式は, ![]() の加法定理
の加法定理![]() と
と![]() を加えます。
を加えます。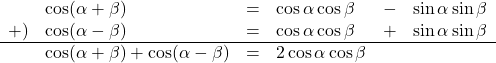
よって, ![]()
最後に![]() の公式は,
の公式は, ![]() の加法定理
の加法定理![]() と
と![]() を引きます。
を引きます。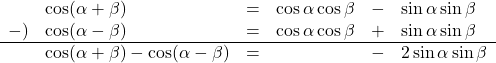
よって, ![]()
数IIIの積分などでも使いますので, 積和の公式は暗記せずとも, 導出はできるようにしておきましょう。そのためにも, 最低限, 加法定理は暗記しましょう。
 数樂管理人のブログ
数樂管理人のブログ 

