こんにちは。今回は指数関数と対数関数の積分について書いておきます。当たり前のことかもしれませんが, 確認の意味も込めて書いておきます。以下, ![]() は積分定数とします。
は積分定数とします。
![]() の積分では,
の積分では, ![]() とおくことで積分しやすくなる。
とおくことで積分しやすくなる。![]() より,
より, ![]() となるので,
となるので, ![]()
となる。
【例】![]() の不定積分を求めよ。
の不定積分を求めよ。
【解法例】![]() とおくと,
とおくと, ![]() なので,
なので, ![]()
したがって, 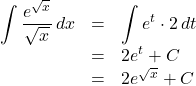
![]() の積分では,
の積分では, ![]() とおくことで積分しやすくなる。
とおくことで積分しやすくなる。![]() より,
より, ![]() となるので,
となるので, ![]() (
(![]() は
は![]() の原始関数)
の原始関数)
【例】![]() の不定積分を求めよ。
の不定積分を求めよ。
【解法例】![]() とおくと,
とおくと, ![]() なので,
なので, ![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int \dfrac{\sqrt[3]{\log{x}}}{x}\,dx&=&\displaystyle\int\sqrt[3]{t}\,dt\\&=&\displaystyle\int t^{\frac13}\,dt\\&=&\dfrac34t^{\frac43}+C\\&=&\dfrac34\log{x}\sqrt[3]{\log{x}}+C\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-f016ed8ab6010ddaa1ed747cfe267fef_l3.png)
まとめ
![]()
![]() の積分では,
の積分では, ![]() とおくことで積分しやすくなる。
とおくことで積分しやすくなる。![]()
![]() の積分では,
の積分では, ![]() とおくことで積分しやすくなる。
とおくことで積分しやすくなる。
 数樂管理人のブログ
数樂管理人のブログ 

