こんにちは。今回は複素数平面で出てくる極形式の表し方について見ていきましょう。
複素数![]() について, これを極方程式で表すとどうなるのか書いていきます。
について, これを極方程式で表すとどうなるのか書いていきます。
先ず![]() の絶対値(実数)を
の絶対値(実数)を![]() とし, 偏角を
とし, 偏角を![]() とすると, 複素数
とすると, 複素数![]() 極形式は,
極形式は, ![]()
で与えられます。
これは, 複素数平面上の点![]() が
が![]() で置き換えることができるので,
で置き換えることができるので, 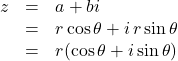
となるからです。(下図参照)

![]() とは複素数平面で複素数
とは複素数平面で複素数![]() が実軸となす角のことを言います。この角を一般に偏角(argument)と言い,
が実軸となす角のことを言います。この角を一般に偏角(argument)と言い, ![]() と表します。また, 偏角
と表します。また, 偏角![]() (
(![]() は整数)です。
は整数)です。
例えば, 偏角![]() の範囲を
の範囲を![]() とし,
とし, ![]() であるなら,
であるなら, ![]() となります。(下図参照)
となります。(下図参照)
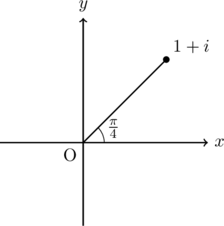
この場合,
一般に, 複素数
となります。
複素数![]() の偏角を求めるとき, 複素数
の偏角を求めるとき, 複素数![]() の絶対値
の絶対値![]() で,複素数
で,複素数![]() を分解します。
を分解します。![]() なので, 複素数
なので, 複素数![]() を次のように分解します。
を次のように分解します。![]()
これが, 極形式![]() と一致することから,
と一致することから, ![]()
![]()
となる偏角![]() を求めるとよい。
を求めるとよい。
次の複素数を極形式で表せ。偏角![]() の範囲は
の範囲は![]() とする。
とする。![]()
![]()
![]()
![]()
![]() より,
より, ![]()
![]() ,
, ![]() となるのは,
となるのは, ![]() のときである。
のときである。
したがって, ![]()
![]() より,
より, 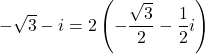
![]() ,
, ![]() となるのは,
となるのは, ![]() のときである。
のときである。
したがって, ![]()
![]() より,
より, ![]()
![]() ,
, ![]() となるのは,
となるのは, ![]() のときである。
のときである。
したがって, ![]()
![]() より,
より, ![]()
![]() ,
, ![]() となるのは,
となるのは, ![]() のときである。
のときである。
したがって, ![]()
 数樂管理人のブログ
数樂管理人のブログ 

