こんにちは。積分方程式を解くときなんかに役立つ知識なので, しっかり身に付けておきたいですね。
以下![]() は
は![]() の関数で,
の関数で, ![]() は関数
は関数![]() の原始関数の1つとする。
の原始関数の1つとする。
定積分で表された関数を微分したときの公式を以下に記す。
![]()
【証明】![]() ただし,
ただし, ![]() は単に定数項であることから, この等式の両辺を
は単に定数項であることから, この等式の両辺を![]() について微分すると,
について微分すると, ![]()
したがって, ![]()
【例】等式![]() を満たす関数
を満たす関数![]() と定数
と定数![]() を求めよ。
を求めよ。
【解答】与式の両辺を![]() について微分すると,
について微分すると, ![]() となる。
となる。
ここで, ![]() として, 与式の両辺に代入すると,
として, 与式の両辺に代入すると,
左辺は![]() になり, 次の
になり, 次の![]() についての二次方程式ができる。
についての二次方程式ができる。![]()
これを解くと, ![]()
よって, ![]()
![]() (答)
(答)
【別解】![]() となるので, 与式の等式の左辺にこれを代入すると,
となるので, 与式の等式の左辺にこれを代入すると, ![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int^{x}_a(2t-5)\,dt&=&\left[t^2-5t\right]^{x}_a\\&=&(x^2-5x)-(a^2-5a)\\&=&x^2-5x-a^2+5a\cdots\maru1\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-968e52bdb3ec072600a895f2d9d5611f_l3.png)
![]() は与式の右辺と恒等的な関係にあるので,
は与式の右辺と恒等的な関係にあるので, ![]() が成り立つ。
が成り立つ。![]()
![]()
よって, ![]()
![]()
【証明】![]()
両辺を![]() について微分すると,
について微分すると, 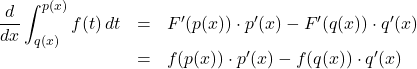
したがって, ![]()
【例】等式![]() を
を![]() について微分せよ。
について微分せよ。
【解答】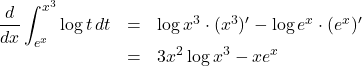
 数樂管理人のブログ
数樂管理人のブログ 

