こんにちは。今回は2次曲線の接線の公式を導いていく問題をやっていきます。
【例】円![]() 上の点
上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】円の方程式の両辺を![]() について微分すると,
について微分すると, ![]()
![]() となり, 点
となり, 点![]() は円周上の点なので,
は円周上の点なので,
接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は, ![]()
これを整理すると, ![]()
となる。
【例】放物線![]() のグラフ上の点
のグラフ上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】放物線の方程式の両辺を![]() について微分すると,
について微分すると, ![]()
![]() となり, 点
となり, 点![]() はグラフ上の点なので,
はグラフ上の点なので,
接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は, ![]()
これを整理すると, ![]()
となる。
【例】楕円![]() 上の点
上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】楕円の方程式の両辺を![]() について微分すると,
について微分すると, ![]()
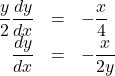
となり, 点![]() は楕円上の点なので,
は楕円上の点なので,
接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は, ![]()
これを整理すると, ![]()
となる。
【例】双曲線![]() 上の点
上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】双曲線の方程式の両辺を![]() について微分すると,
について微分すると, ![]()
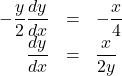
となり, 点![]() は双曲線上の点なので,
は双曲線上の点なので,
接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は, ![]()
これを整理すると, ![]()
となる。
【問1】円![]() 上の点
上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】円の方程式の両辺を![]() について微分すると,
について微分すると,![]()
![]() となり, 点
となり, 点![]() は円周上の点なので,
は円周上の点なので,![]() が成り立つ。
が成り立つ。
また, 接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は,![]()
これを整理すると,![]()
となり, ![]() から, 接線の方程式は,
から, 接線の方程式は,![]() となる。
となる。
【問2】放物線![]() 上の点
上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】放物線の方程式の両辺を![]() について微分すると,
について微分すると,![]()
![]() となり, 点
となり, 点![]() はグラフ上の点なので,
はグラフ上の点なので,![]() が成り立つ。
が成り立つ。
また, 接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は,![]()
これを計算すると,![]()
![]() から,
から,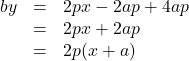
よって, 接線の方程式は,![]()
となる。
【問3】楕円![]() 上の点
上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】楕円の方程式の両辺を![]() について微分すると,
について微分すると,![]()
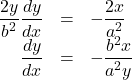
となり, 点![]() は楕円上の点なので,
は楕円上の点なので,![]() が成り立つ。
が成り立つ。
また, 接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は,![]()
これを計算すると,![]() となり,
となり, ![]() より,
より,
両辺を![]() で割ると,
で割ると,![]()
![]() より, 接線の方程式は,
より, 接線の方程式は, ![]()
となる。
【問4】双曲線![]() 上の点
上の点![]() における接線の方程式は,
における接線の方程式は, ![]() で表されることを示せ。
で表されることを示せ。
【解答例】楕円の方程式の両辺を![]() について微分すると,
について微分すると, ![]()
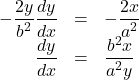
となり, 点![]() は楕円上の点なので,
は楕円上の点なので, ![]() が成り立つ。
が成り立つ。
また, 接線の傾きは![]() となる。
となる。
したがって, 点![]() における接線の方程式は,
における接線の方程式は, ![]()
これを計算すると, ![]() となり,
となり, ![]() より,
より,
両辺を![]() で割ると,
で割ると, ![]()
![]() より, 接線の方程式は,
より, 接線の方程式は, ![]()
となる。
 数樂管理人のブログ
数樂管理人のブログ 

