こんにちは。今回は台形の面積の二等分線ということで, 第一弾に続き, 第二弾をお届けします。
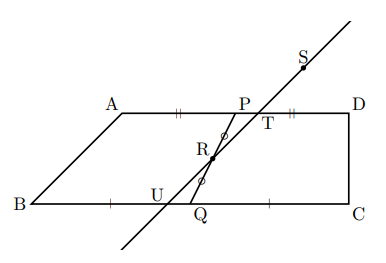
台形の面積を二等分するときは, どの点を通るのでしょうか。右の台形ABCD(AD![]() BC)を点Sを通る直線で, 面積を二等分することを考える。
BC)を点Sを通る直線で, 面積を二等分することを考える。
ここで, 図中の点Pは辺ADの中点, 点Qは辺BCの中点で, 点Rは線分PQの中点である。このとき, 点Sと点Rを結ぶ線分が台形の面積を二等分する式である。
理由は台形の面積を二等分するには, 二等分された図形の上底![]() 下底が等しいことが前提である。点P, Qを各辺の中点としたのはそのためである。そして, 点Rを線分PQの中点とすることで, 点Sから点Rを通る直線とでできる△TRPと△URQは合同になり, 面積が等しいので, 面積が等しいことが保たれる。結果, 四角形
下底が等しいことが前提である。点P, Qを各辺の中点としたのはそのためである。そして, 点Rを線分PQの中点とすることで, 点Sから点Rを通る直線とでできる△TRPと△URQは合同になり, 面積が等しいので, 面積が等しいことが保たれる。結果, 四角形![]() 四角形
四角形![]() となる。ただし, 点T, Uは直線SRと各辺との交点である。
となる。ただし, 点T, Uは直線SRと各辺との交点である。
まぁ上底と下底の比を分ければ問題はないかと思うが, こちらの方が取り組みやすい例を挙げて問題を解いてみます。第一弾の台形の面積の攻略とはまた違う観点でお楽しみください。
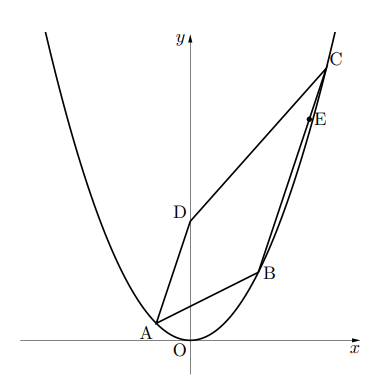
右の図において, 曲線アは関数![]() のグラフであり, 点A, B, C, Dの
のグラフであり, 点A, B, C, Dの![]() 座標はそれぞれ,
座標はそれぞれ, ![]() で, AD
で, AD![]() BCである。
BCである。
このとき, 直線BC上の点E(7, 13)をとおり, 四角形ABCDの面積を二等分する式を求めなさい。
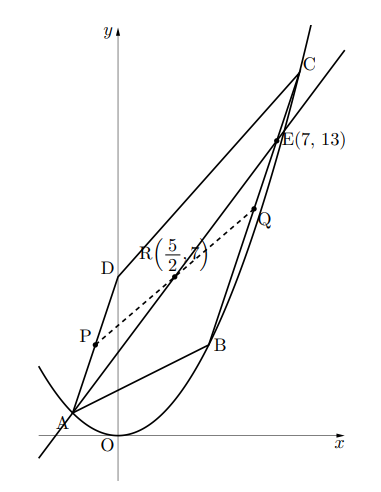
問題より, A![]() , B(4, 4), C(8, 16), D(0, 7)である。ここで, 四角形ABCDは台形であるから, 線分ADの中点P
, B(4, 4), C(8, 16), D(0, 7)である。ここで, 四角形ABCDは台形であるから, 線分ADの中点P![]() , 線分BCの中点Q(6, 10)であるから, 線分PQの中点Rの座標は
, 線分BCの中点Q(6, 10)であるから, 線分PQの中点Rの座標は![]() である。よって求める直線の式は,2点E, Rを通る式で,
である。よって求める直線の式は,2点E, Rを通る式で,
その式は![]() であり, これはA
であり, これはA![]() を通る直線なので, 条件を満たす。
を通る直線なので, 条件を満たす。
台形の面積の二等分は上底の中点と下底の中点を結ぶ中点を通る。
 数樂管理人のブログ
数樂管理人のブログ 


台形の面積の二等分線②の台形問題についてですが教えてください。
Eをとおる二等分線は台形のもう一方の底辺(両端を含む)を通る必要がありますが、求めた直線式がこの条件を満たしている事の確認はしなくてもよいのでしょうか?
それとも、直線上の一点が一つの底辺上にあり(この問題の場合E)、中点の中点Rを通るときは必ず他方の底辺を通るものなんでしょうか?
宜しくお願いいたします。
モリヤンさん
ご指摘ありがとうございます。確認は必要ですね。
一部加筆いたしましたので、ご確認いただけたらと存じます。
また何かございましたらご指摘お願いいたします。
ありがとうございます。