こんにちは。今回は三角形の面積の2等分と四角形の面積を分ける問題を扱っていきます。それではいきましょう。
三角形の面積の2等分の式を求めるときは,
【パターン1】三角形の頂点を通る場合
【パターン2】三角形の頂点を通らない場合
に大別できます。
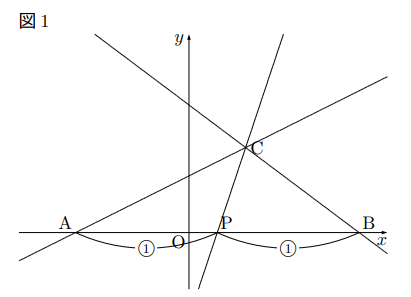
問題の点Cは△ABCの頂点の1つ。頂点を通る場合は, その頂点と向かい合う辺の中点P(真ん中の点)を通る直線の式を求めれば片付きます。これは高さが共通の三角形の面積が底辺の比の割合によって分けられるからです。
そこで, 点A, B, Cの座標を求めると, ![]() ,
, ![]() ,
, ![]()
ABの中点PはAとBの座標を筆算で足すと(2, 0), 中点Pはその![]() (半分)なので, P(1, 0)となる。よって求める直線CPの式は
(半分)なので, P(1, 0)となる。よって求める直線CPの式は![]() となります。
となります。
2点P![]() , Q
, Q![]() の中点の座標R
の中点の座標R
R![]()
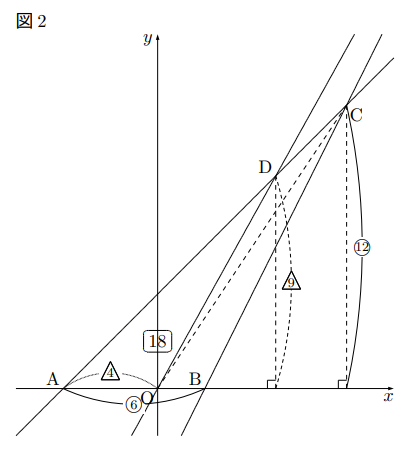
こんな場合はとりあえず, A, B, Cの座標を出し, △ABCの面積を求める。今回の場合, ![]() ,
, ![]() ,
, ![]() であるから, △ABCの面積は
であるから, △ABCの面積は![]() 。
。
次に, 原点とCを結んでみると, 面積は, △![]() △
△![]() であるから, 面積を二等分する直線を求めるために必要なもう1点Dは
であるから, 面積を二等分する直線を求めるために必要なもう1点Dは![]() 上にある。また, △OADの面積は36の半分18になればよい。ここで, △OADの底辺OAの長さはAの座標からも分かるとおり4であるから, 求める高さをD
上にある。また, △OADの面積は36の半分18になればよい。ここで, △OADの底辺OAの長さはAの座標からも分かるとおり4であるから, 求める高さをD![]() とすると,
とすると, ![]()
これから, ![]()
この![]() がDの
がDの![]() 座標でDは
座標でDは![]() 上にあることから,
上にあることから, ![]() とおいて,
とおいて, ![]() を求めると,
を求めると, ![]()
よってD(5, 9)となり, 求める直線の式は![]() となる。
となる。
今までのは基本で, 四角形の面積を分ける考え方に利用します。四角形の捉え方は別の攻略方法でもお知らせしていますが, 三角形が2つで四角形として捉えるのが大体の考え方です。
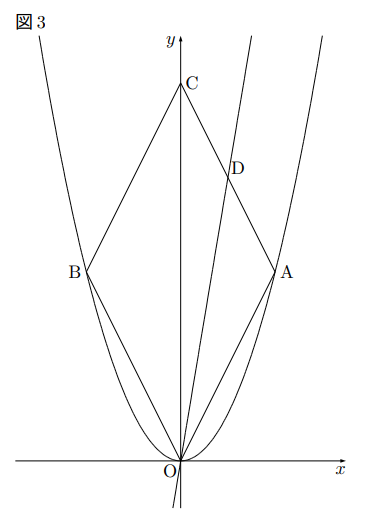
【例】図3は関数![]() のグラフで, ABは
のグラフで, ABは![]() 軸に平行でその長さは8です。四角形OABCがひし形のとき, 辺AC上に点Dをとり, △OADと四角形OBCDの面積比が
軸に平行でその長さは8です。四角形OABCがひし形のとき, 辺AC上に点Dをとり, △OADと四角形OBCDの面積比が![]() となる, 直線ODの式を求めなさい。
となる, 直線ODの式を求めなさい。
(類高知)
【考え方】
この問題では四角形OABC(ひし形OABC)の面積はOCによって二等分されるので, その半分を, ![]() より
より![]() とおきます。すると, 求めるDはACの中点であることがわかります。なぜならDがACの中点であることで, △OCD : △OAD
とおきます。すると, 求めるDはACの中点であることがわかります。なぜならDがACの中点であることで, △OCD : △OAD![]() となり, 四角形
となり, 四角形![]() △OBC
△OBC![]() △OCD
△OCD![]() となり, 問題にあるように, △OADと四角形OBCDの面積比が
となり, 問題にあるように, △OADと四角形OBCDの面積比が![]() となります。
となります。
【解法】
A(4, 8), C(0, 16)よりD(2, 12)であるから, 求める式は![]() である。
である。
 数樂管理人のブログ
数樂管理人のブログ