こんにちは。今回は数列の極限について書いておきます。
限りなく続く数列を無限数列という。無限数列![]() において,
において, ![]() を限りなく大きくしたときの
を限りなく大きくしたときの![]() の値を調べることを, 数列
の値を調べることを, 数列![]() の極限を調べるという。ただし,
の極限を調べるという。ただし, ![]() は自然数。
は自然数。
![]() 収束
収束![]() が定数
が定数![]() に限りなく近づく。この
に限りなく近づく。この![]() を極限値という。
を極限値という。![]()
![]() 発散
発散
正の無限大に発散![]() が限りなく大きくなる。
が限りなく大きくなる。![]()
負の無限大に発散![]() が限りなく小さくなる。
が限りなく小さくなる。![]()
振動![]() 値が上下するとき極限値はない。例:
値が上下するとき極限値はない。例:![]() のような数列
のような数列
数列![]() ,
, ![]() が収束し,
が収束し, ![]() ,
, ![]() のとき,
のとき, ![]()
![]() (
(![]() は定数)
は定数)![]()
![]()
![]()
![]()
![]()
![]()
![]()
不定形![]() ,
, ![]() のとき,
のとき, ![]() ,
, ![]()
が成り立つが, ![]()
![]()
の極限にはいろいろ考えられる。これらを不定形という。
![]()
![]() の不定形では,
の不定形では, ![]() の最高次数でくくって極限をとるとよい。
の最高次数でくくって極限をとるとよい。![]()
![]() の不定形では,
の不定形では, ![]() の
の![]() の最高次数で分母分子を割って極限をとるとよい。
の最高次数で分母分子を割って極限をとるとよい。
無理式の極限では以下のことに着眼して解くとうまくいくことが多い。
無理式の極限では, 分母や分子の有理化を行うとよい。
以下分子の有理化のイメージ![]() の場合
の場合![]() として, 分母分子に
として, 分母分子に![]() をかける。
をかける。
つまり,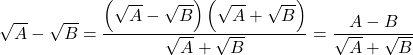
として,![]() で極限を求めるとよい。
で極限を求めるとよい。
次の数列の極限を調べよ。
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(1) ![]() で,
で, ![]() を
を![]() にすると,
にすると, ![]() は限りなく0に近づくので,
は限りなく0に近づくので, ![]() は2に収束する。したがって, 極限値は2
は2に収束する。したがって, 極限値は2
(2) ![]() で,
で, ![]() を
を![]() にすると, いずれ
にすると, いずれ![]() となり, どんどん小さくなっていく。したがって, この数列は
となり, どんどん小さくなっていく。したがって, この数列は![]() に発散する。
に発散する。
(3) ![]() の
の![]() を
を![]() にすると, 数はどんどん大きくなっていく, したがって, この数列は
にすると, 数はどんどん大きくなっていく, したがって, この数列は![]() に発散する。
に発散する。
(4) この数列は正の項, 負の項が交互に現れるので, ![]() にも
にも![]() にも発散しない。ゆえにこの数列は振動する。
にも発散しない。ゆえにこの数列は振動する。
次の極限を調べよ。
(1) ![]()
(2) ![]()
(3) ![]()
(1) 分子分母を![]() で割る。
で割る。![]()
(2) 分子分母を![]() で割る。
で割る。![]()
(3) 分子分母を![]() で割る。
で割る。![]()
![]() の極限値を求めよ。
の極限値を求めよ。
分子の有理化を行う。![]() と考えて, 分母分子に
と考えて, 分母分子に![]() をかける。
をかける。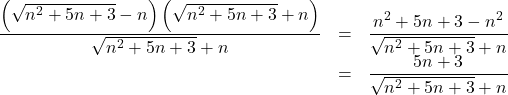
これを用いて, 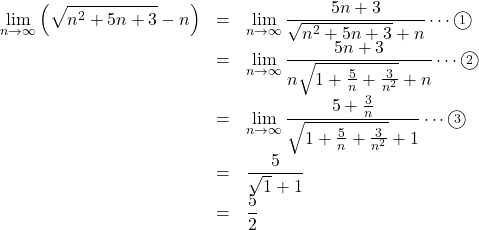
![]() の分母の
の分母の![]() の中を
の中を![]() でくくって,
でくくって, ![]() を
を![]() の外へ出すと
の外へ出すと![]() になる。
になる。![]() の分母分子を
の分母分子を![]() で割って,
で割って, ![]() にするという流れ。
にするという流れ。
 数樂管理人のブログ
数樂管理人のブログ 

