こんにちは。今回は極限のところでよく出題される場合分けの問題についてです。
【例題】![]() を正の定数とするとき,
を正の定数とするとき, ![]() を求めよ。
を求めよ。
【解法のための思考】![]() と
と![]() の大小関係が攻略のカギとなります。それは以下の関係が成り立つからです。
の大小関係が攻略のカギとなります。それは以下の関係が成り立つからです。 ![]()
![]() なら,
なら, ![]() となるため,
となるため, ![]()
![]()
![]() なら,
なら, ![]() となるため,
となるため, ![]()
![]()
![]() なら,
なら, ![]() となるため,
となるため, ![]()
この3パターンに場合分けして解答していくのが, この手の問題の攻略のポイントになります。
【解答例】![]()
![]() のとき,
のとき, 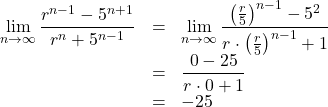
![]()
![]() のとき,
のとき, 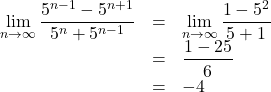
![]()
![]() のとき,
のとき, 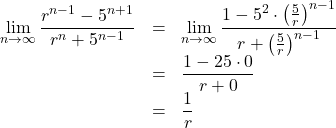
![]() を正の定数とするとき,
を正の定数とするとき, ![]() を求めよ。
を求めよ。
![]() と
と![]() の大小関係に着目して場合分けを行う。
の大小関係に着目して場合分けを行う。![]()
![]() のとき,
のとき, ![]()
![]()
![]() のとき,
のとき, ![]()
![]()
![]() のとき,
のとき, 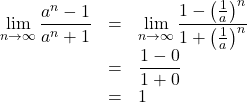
 数樂管理人のブログ
数樂管理人のブログ 

