こんにちは。今回は無限級数について書いておきます。
無限級数とは![]() を無限級数という。
を無限級数という。
部分和について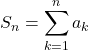 をこの無限級数の初項から第
をこの無限級数の初項から第![]() 項までの部分和という。
項までの部分和という。![]() なら, この無限級数は収束して和
なら, この無限級数は収束して和![]() をもつ。
をもつ。
数列![]() が発散するなら, この無限級数は発散するという。
が発散するなら, この無限級数は発散するという。
【例】無限級数![]() の収束, 発散を調べ, 収束するときは, その和を求めよ。
の収束, 発散を調べ, 収束するときは, その和を求めよ。
【解法例】無限和を考えるのも部分和の延長なので, 部分和を考える考え方でいく。したがってこの場合, 部分分数分解して考えることにする。
問題の部分和![]() は,
は, 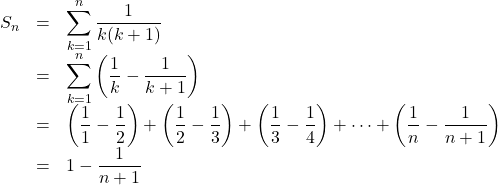
よって, ![]()
ゆえに, この無限級数は収束し, その和は1になる。
【例】無限級数![]() の収束, 発散を調べ, 収束するときは, その和を求めよ。
の収束, 発散を調べ, 収束するときは, その和を求めよ。
【解法例】分母の有理化をして考える。![]()
なので, これを用いて部分和を考えると, 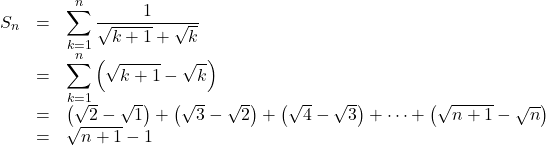
よって, ![]()
ゆえに, この無限級数は発散する。
 数樂管理人のブログ
数樂管理人のブログ 

