こんにちは。今回は無限級数の収束条件を用いた問題です。それでは問題を見ていきましょう。
【例】無限等比級数![]()
について, 次の問いに答えよ。
(1) この級数が収束するための実数![]() の範囲を求めよ。
の範囲を求めよ。
(2) ![]() が(1)の範囲にあるとき, この級数の和を求めよ。
が(1)の範囲にあるとき, この級数の和を求めよ。
(3) (2)で求めた和を関数![]() とするとき, それを図示せよ。
とするとき, それを図示せよ。
【解答例】
(1) この級数は, 初項![]() , 公比
, 公比![]() であり,
であり, ![]() なので, この級数が収束する条件は, 初項が
なので, この級数が収束する条件は, 初項が![]() か, 公比の絶対値が
か, 公比の絶対値が![]() より小さいかになる。公比に関しては,
より小さいかになる。公比に関しては, ![]() から
から![]() より大きいことがわかっている。したがって,
より大きいことがわかっている。したがって, ![]() ,
, ![]()
が求める条件になる。![]() のとき,
のとき, ![]() より,
より, ![]()
![]() のとき, 分母が1より大きいことが条件になるので,
のとき, 分母が1より大きいことが条件になるので, ![]()
![]()
![]()
よって, ![]()
以上より, 求める条件は, ![]() (答)
(答)
(2) ![]() のとき, (初項)
のとき, (初項)![]() より, 和は
より, 和は![]()
![]() のとき, 和は,
のとき, 和は, 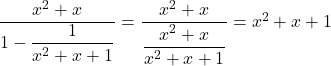
以上より, ![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
(3) (2)より, ![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
としてグラフを描くと,

チェック
無限級数の収束条件を絡める問題は多いので押さえておきましょう。
 数樂管理人のブログ
数樂管理人のブログ 

