こんにちは。今回は無限級数の収束, 発散の判定法について書いておきます。を
無限級数の部分和![]() が求まれば,
が求まれば, ![]() が, 一定の数
が, 一定の数![]() になるなら, 収束するし, それ以外なら発散することになる。
になるなら, 収束するし, それ以外なら発散することになる。
このとき, ![]() が収束するならば,
が収束するならば, ![]()
が言える。以下に証明を記す。
【証明】![]() が収束するとして, その和を
が収束するとして, その和を![]() とおく。また, 部分和
とおく。また, 部分和![]() を,
を, 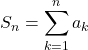 とすると,
とすると, ![]() であるから,
であるから, ![]() (証明終)
(証明終)
また, ![]() の対偶は,
の対偶は,
無限級数![]() が
が![]() に収束しないとき,
に収束しないとき, ![]() は発散する。
は発散する。
であり, この証明からこのことも言える。
上の![]() で逆は成り立たないということです。
で逆は成り立たないということです。![]() の逆は,
の逆は, ![]() ならば,
ならば, ![]() は収束する。
は収束する。
ですが, 感覚的には![]() がどんどん小さくなっていくことで, 間違いないですが, それで収束するかというと, そうではありません。
がどんどん小さくなっていくことで, 間違いないですが, それで収束するかというと, そうではありません。
反例はこちらから抜粋して以下に書く。
【例】無限級数![]() の収束, 発散を調べ, 収束するときは, その和を求めよ。
の収束, 発散を調べ, 収束するときは, その和を求めよ。
【着眼】問題の![]() は, 明らかに,
は, 明らかに, ![]() だが, 以下のように
だが, 以下のように![]() に発散する。
に発散する。
【解法例】分母の有理化をして考える。![]()
なので, これを用いて部分和を考えると, 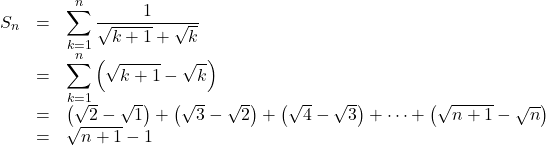
よって, ![]()
ゆえに, この無限級数は発散する。
 数樂管理人のブログ
数樂管理人のブログ 

